電験三種 H28年 機械 問14 問題と解説

　問 題　　　　　

次の文章は、基数の変換に関する記述である。

• 2進数00100100を10進数で表現すると(　ア　)である。
• 10進数170を2進数で表現すると(　イ　)である。
• 2進数111011100001を8進数で表現すると(　ウ　)である。
• 16進数(　エ　)を2進数で表現すると11010111である。

上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

　　(ア)　　　(イ)　　　　(ウ)　　(エ)

1. 36　　10101010　　7321　　D7
2. 37　　11010100　　7341　　C7
3. 36　　11010100　　7341　　D7
4. 36　　10101010　　7341　　D7
5. 37　　11010100　　7321　　C7

 

 

 

 

 

　解 説　　　　

(　ア　)について、(00100100)₂を10進数に直す際には、2進数の一の位が2の0乗、十の位が2の1乗、百の位が2の2乗…と対応していきます。つまり、以下の図のように書くことができます。

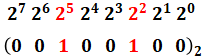
よって、これを計算すると、次の通りとなります。

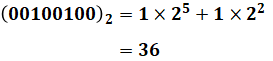
(　イ　)について、10進数を2進数にするには、以下のように元の数字(10進数の数値)を2でどんどん割っていって、その余りを下から上へ読んでいったものが答えとなります。

よって、(170)₁₀=(10101010)₂だとわかります。

(　ウ　)について、8は2の3乗なので、2進数が3桁分で、8進数の1桁に相当すると考えてください。つまり、

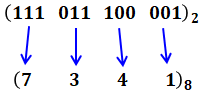
上記のようになります。3桁ずつの中での数値の出し方は、2進数を10進数に直すときと一緒です。つまり、1番左側の(111)₂なら、「1×2²+1×2¹+1×2⁰=7」といった具合です。

(　エ　)について、これも(　ウ　)のときとほとんど一緒ですが、16は2の4乗なので、2進数が4桁分で16進数の1桁に相当します。

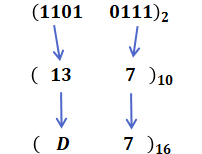
(　ウ　)のときは2進数を直接8進数に直しましたが、16進数はアルファベットが入ってわかりにくいので、上記のように一旦10進数にしています(しなくても構いません)。ちなみに、(1101)₂が13になるのは、「1×2³+1×2²+1×2⁰=13」という理屈です。

ここで、16進数は10進数でいう「0から15まで」を1桁で表していますが、0～9は10進数と同じで、それ以降は、(10)₁₀=(A)₁₆、(11)₁₀=(B)₁₆、(12)₁₀=(C)₁₆、(13)₁₀=(D)₁₆、(14)₁₀=(E)₁₆、(15)₁₀=(F)₁₆と表現します。よって、(　エ　)には「D7」が入ります。