電験三種 H28年 電力 問17 問題と解説

　問 題　　　　　

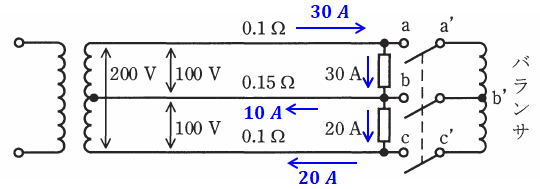
図のような、線路抵抗をもった100/200V単相3線式配電線路に、力率が100%で電流がそれぞれ30A及び20Aの二つの負荷が接続されている。この配電線路にバランサを接続した場合について、次の(a)及び(b)の問に答えよ。

ただし、バランサの接続前後で負荷電流は変化しないものとし、線路抵抗以外のインピーダンスは無視するものとする。

(a)　バランサ接続後a’-b’間に流れる電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 5
2. 10
3. 20
4. 25
5. 30

(b)　バランサ接続前後の線路損失の変化量の値[W]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 20
2. 65
3. 80
4. 125
5. 145

 

 

 

 

 

　解 説　　　　

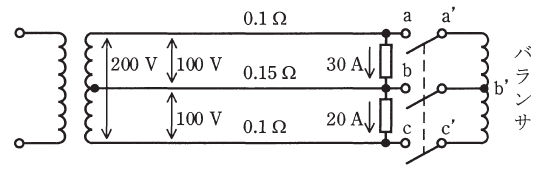
バランサというのは、単相3線式配電線路の受電端に取り付ける、巻数1：1の単巻変圧器のことです。これを接続することによって、以下の図のように、接続前には中性線へ流れていた分の電流がバランサのほうに移ることで、中性線に電流が流れなくなります。

ちなみに、バランサは必ず巻数が1：1なので、点b’から上下に流れる電流I₃は同じ大きさです。

バランサを接続すると、このように中性線に電流が流れなくなるので、その分、線路損失が減るというメリットがあります。これが問題(b)の主旨となっています。

(a)

先ほどの回路図を再び載せますので、これを見ながら考えてください。

求めたいのは上記のうちI₃ですが、すでにI₁=30A、I₂=20Aで、中性線には電流が流れないとわかっているので、b-b’間を流れる電流2I₃は、

となります。よって、求める答えは、

と計算できます。

(b)

(b)はバランサ接続前後の変化量が問われているので、まずは(a)の流れのまま、接続後について考えます。

線路損失というのは、3線それぞれの損失(電流²×抵抗)の和となるので、バランサ接続後の線路損失P_afterは、

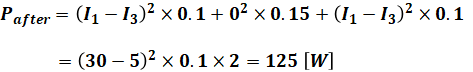
となります。

一方、バランサ接続前の線路損失P_beforeは次のようになります。

以上から、線路損失の変化量ΔPは、

と計算することができます。