問 題
演算増幅器(オペアンプ)について、次の(a)及び(b)の問に答えよ。
(a) 演算増幅器は、その二つの入力端子に加えられた信号の( ア )を高い利得で増幅する回路である。演算増幅器の入力インピーダンスは極めて( イ )ため、入力端子電流は( ウ )とみなしてよい。
一方、演算増幅器の出力インピーダンスは非常に( エ )ため、その出力端子電圧は負荷による影響を( オ )。さらに、演算増幅器は利得が非常に大きいため、抵抗などの部品を用いて負帰還をかけたときに安定した有限の電圧利得が得られる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ) (オ)
- 差動成分 大きい ほぼ零 小さい 受けにくい
- 差動成分 小さい ほぼ零 大きい 受けやすい
- 差動成分 大きい 極めて大きな値 大きい 受けやすい
- 同相成分 大きい ほぼ零 小さい 受けやすい
- 同相成分 小さい 極めて大きな値 大きい 受けにくい
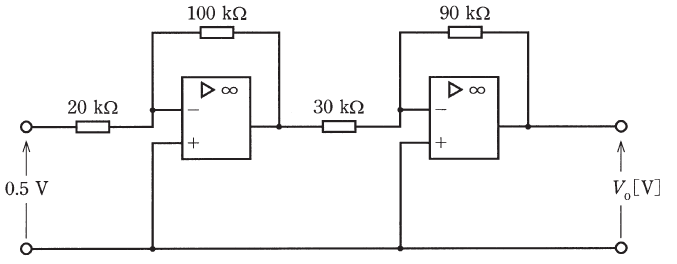
(b) 図のような直流増幅回路がある。この回路に入力電圧0.5Vを加えたとき、出力電圧Voの値[V]と電圧利得Avの値[dB]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、演算増幅器は理想的なものとし、log102=0.301、log103=0.477とする。
Vo Av
- 7.5 12
- -15 12
- -7.5 24
- 15 24
- 7.5 24
解 説
(a)
演算増幅器は入力端子の信号の差動成分を増幅する装置であるため、( ア )には「差動成分」が入ります。差動成分とは、問題文の図でいう-端子と+端子の電圧差のことです。
理想的な演算増幅器においては入力インピーダンスが無限大ということになっているので、入力端子に電流はほとんど流れません。問題文の図では「▷∞」と表示されていますが、これが入力インピーダンスが無限大であることを表しています。よって、( イ )には「大きい」が、( ウ )には「ほぼ零」が入ります。
反対に、出力インピーダンスはほぼ0なので、電流は損失なく流れることができるので、出力端子電圧は負荷による影響をほとんど受けないことになります。よって、( エ )には「小さい」が、( オ )には「受けにくい」が入ります。
以上から、(a)の正解は(1)となります。
(a)の問題文は演算増幅器の基本的な説明文になっていて、これを押さえておくことは理論分野だけでなく、機械分野においても有用です。特に「入力インピーダンスが無限大」あたりは重要事項としてしっかり押さえておいてください。
(b)
Voを求める際は、問題文の図を直接使うのではなく、2つの演算増幅器を分けて扱うほうが考えやすいと思います。
まずは入力電圧(0.5V)を含む演算増幅器だけを取り出すと、以下の図のようになります。
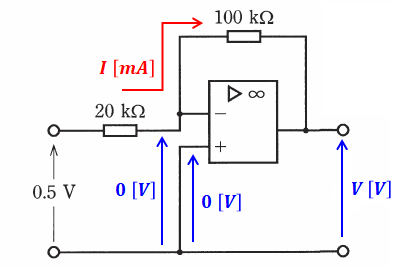
上図において、図の最下線(接地面)から+端子までの間に抵抗はないので、当然、ここは0[V]となります。また、(a)の通り、前提条件として入力インピーダンスは∞で入力端子電流が0なので、接地面から-端子までの電圧差も同じく0[V]となります。
すると、0.5[V]の入力電圧が20[kΩ]の抵抗を通ると0[V]まで下がるため、ここを流れる電流Iは
![]()
となります(抵抗の単位が[kΩ]なので、電流の単位は[mA]になります)。さらに100[kΩ]の抵抗を経るとV[V]になりますが、流れる電流は変わらないので、
![]()
となります。
ちなみに、今回のように入力端子が-端子とつながっている場合には、上記のように入力(+0.5[V])と出力(-2.5[V])の符号(+or-)が反転します。もし入力端子が+端子とつながっているなら、このような符号の反転は起こりません。
ここまで読んで、勘の良い人はお気づきだと思いますが、この演算増幅器によって0.5[V]で入ったものが-2.5[V]で出るということは、上記のような計算をせずに暗算で解くこともできます。
最初の抵抗が20[kΩ]で次の抵抗が100[kΩ]なので、この比が5倍であることから、入力電圧を5倍して符号を反転させると出力電圧となる、という考え方が成り立ちます。
この考え方を使って2つ目の演算増幅器について考えると、入力電圧(=1つ目の演算増幅器の出力電圧)が-2.5[V]で、90/30=3倍の増幅に対して符号を反転させればよいので、その出力電圧Voは、
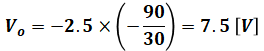
となります。
続いて電圧利得AVの計算ですが、以下の式を公式として覚えておくことをおすすめします。
![]()
- Vin:入力電圧[V]
- Vout:出力電圧[V]
上式に今までの計算結果を代入すると、
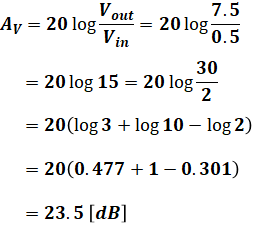
のように計算することができます。
(以下、参考)
ちなみに、上で示した公式を覚えていない場合でも、単位が[dB]ということから、音圧レベルの公式を思い出すことができれば、以下のような式変換により上記の公式を導出することもできます(ただし、重要事項なので公式をそのまま覚えたほうが有用だとは思います)。
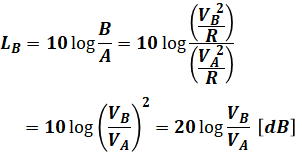
- LB:音圧レベル[dB]
- A:基準となるエネルギー[W]
- B:比較する側のエネルギー[W]

コメント