電験三種 H27年 機械 問15 問題と解説

　問 題　　　　　

定格出力15kW、定格電圧220V、定格周波数60Hz、6極の三相巻線形誘導電動機がある。二次巻線は星形(Y)結線でスリップリングを通して短絡されており、各相の抵抗値は0.5Ωである。この電動機を定格電圧、定格周波数の電源に接続して定格出力(このときの負荷トルクをT_nとする)で運転しているときの滑りは5%であった。

計算に当たっては、L形簡易等価回路を採用し、機械損及び鉄損は無視できるものとして、次の(a)及び(b)の問に答えよ。

(a)　速度を変えるために、この電動機の二次回路の各相に0.2Ωの抵抗を直列に挿入し、上記と同様に定格電圧、定格周波数の電源に接続して上記と同じ負荷トルクT_nで運転した。このときの滑りの値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 3.0
2. 3.6
3. 5.0
4. 7.0
5. 10.0

(b)　電動機の二次回路の各相に上記(a)と同様に0.2Ωの抵抗を直列に挿入したままで、電源の周波数を変えずに電圧だけを200Vに変更したところ、ある負荷トルクで安定に運転した。このときの滑りは上記(a)と同じであった。

この安定に運転したときの負荷トルクの値[N・m]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 99
2. 104
3. 106
4. 109
5. 114

 

 

 

 

 

　解 説　　　　

(a)

巻線形誘導電動機のトルクT_nは、二次回路の巻線抵抗r₂と滑りsの比に関係した値をとります。つまり、トルクT_nが一定という条件のもとでは、巻線抵抗r₂と滑りsの比は常に一定となります。

• r₂：二次巻線抵抗[Ω]
• s：滑り
• const.：一定、という意味(コンスタントの略)

たとえば、r₂を3倍にしたらsも3倍になるので、このような特性を「比例推移」といいます。この特性は、巻線形誘導電動機の始動トルクの改善や速度制御に広く利用されています。

今回の問題ではr₂を0.5Ωから0.7Ω(=0.5+0.2)に変更しているため、変更後の滑りs’は次のように計算できます。

(b)

電圧が変化したときのトルクを求める問題ですが、まず、重要事項として、トルクは電圧の2乗に比例します。これはそのまま知識として押さえておいてもよいですが、トルクTと二次入力P₂との関係式から考えることもできます。

• P₂：二次入力[W]
• ω：角速度[rad/s]
• T：トルク[N・m]
• V：電源電圧[V]
• Z：インピーダンス[Ω]
• N_s：同期速度[min^-1]

上式の矢印左側は、最重要公式として押さえてください。矢印右側は、二次入力と角速度をそれぞれ変形したものですが、ZやN_sは一定なので、TはVの2乗に比例することがわかります(N_sは磁極の数と周波数から決まる値なので、今回はこれらに変更がないため、一定となります)。

この問題は電圧変更後のトルクを求めるのが目的ですが、すでに変更前後の電圧はわかっているので、変更前のトルクさえわかれば解くことができます。

電圧変更前のトルクTは上式を使うと次のように表すことができます。

ここで、同期速度N_sは磁極の数pと周波数fから計算できるので、次のようになります。

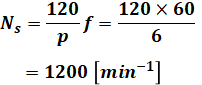
また、上式では二次入力P₂が書かれていますが、問題文で与えられているのは定格出力(機械出力)P_mです。

二次入力P₂と機械出力P_mとの関係を表す式は、以下の通りです。

よって、以上の2つの式から電圧変更前のトルクTの値を求めることができます。

以上から、電圧変更後のトルクT’は、

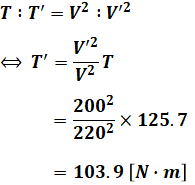
と計算することができます。