問 題
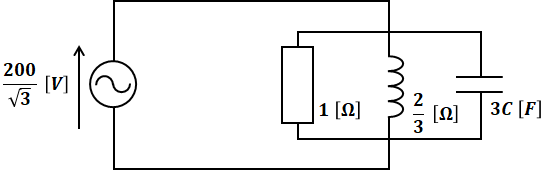
図1のように、線間電圧200V、周波数50Hzの対称三相交流電源に1Ωの抵抗と誘導性リアクタンス4/3Ωのコイルとの並列回路からなる平衡三相負荷(Y結線)が接続されている。また、スイッチSを介して、コンデンサC(Δ結線)を接続することができるものとする。次の(a)及び(b)の問に答えよ。
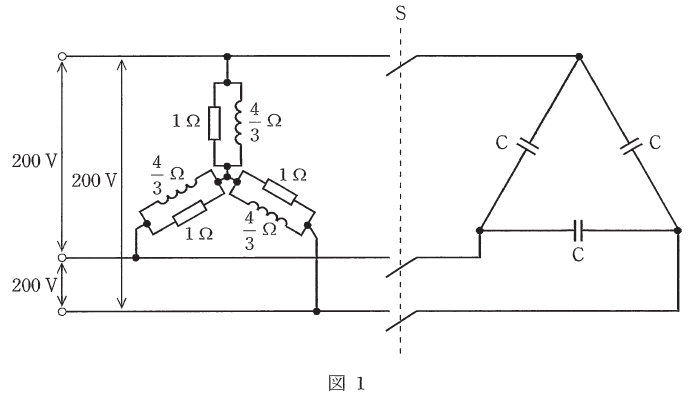
(a) スイッチSが開いた状態において、三相負荷の有効電力Pの値[kW]と無効電力Qの値[kvar]の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
P Q
- 40 30
- 40 53
- 80 60
- 120 90
- 120 160
(b) 図2のように三相負荷のコイルの誘導性リアクタンスを2/3Ωに置き換え、スイッチSを閉じてコンデンサCを接続する。このとき、電源からみた有効電力と無効電力が図1の場合と同じ値となったとする。コンデンサCの静電容量の値[μF]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
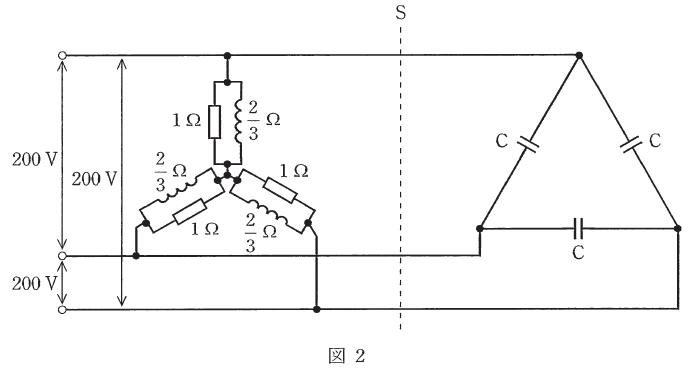
- 800
- 1200
- 2400
- 4800
- 7200
解 説
(a)
スイッチSが開いているので、ここでは図中の左側部分だけ考えればよいです。Y結線の中心から中性線を引いて1相あたりの等価回路を取り出すと、相電圧は線間電圧の√3分の1倍になるので、その回路図は以下のように描くことができます。
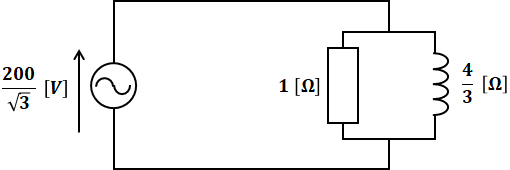
このうち、抵抗で消費される電力が有効電力Pで、コイルで消費される電力が無効電力Qなので、PとQはそれぞれ以下のように計算することができます。
ちなみに、以下の式の係数である3は、設問で三相分の電力が問われているので3倍しています。
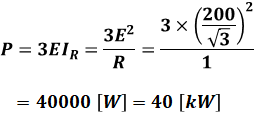
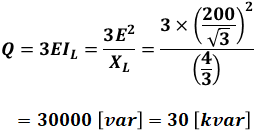
- E:相電圧[V]
- IR:抵抗を流れる電流[A]
- IL:コイルを流れる電流[A]
- R:抵抗[Ω]
- XL:コイルのリアクタンス[Ω]
(b)
図2は左側がY結線で右側がΔ結線なので、このままでは計算しづらいため、右側をY結線に変換します(左側をΔ結線にして統一しても構いませんが、Y結線で揃えたほうが中性点を使った等価回路が描けて便利なので、Y結線に統一するほうが解きやすいと思います)。
Δ結線→Y結線の変換により、コンデンサの静電容量は3倍になるので、スイッチを閉じたあとの1相あたりの等価回路は次のようになります。
抵抗のほうは図1でも図2でも特に変化がないので有効電力が同じなのは当然で、抵抗については考える必要がありません。無効電力は(a)で計算したように端子電圧(=相電圧)とリアクタンスの値によって決まりますが、電圧は(a)のときと変わっていないので、要するに注目すべきはリアクタンスということになります。
よって、(a)で紹介した等価回路でのコイルのリアクタンスと、上図の等価回路でのコイル及びコンデンサの合成リアクタンスが一致すれば、図1と図2とでの無効電力も一致するといえます。
コイルとコンデンサが並列に並んでいるとき、その合成リアクタンスの逆数は、各々のリアクタンスの逆数の和となり、この合成リアクタンスの値が図1のコイルのリアクタンス4/3[Ω]と一致するので、
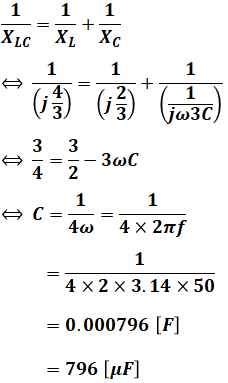
- XLC:合成リアクタンス[Ω]
- XL:コイルのリアクタンス[Ω]
- XC:コンデンサのリアクタンス[Ω]
- ω:角周波数[rad/s] (=2πf)
- f:周波数[Hz]
と計算することができます。

コメント