問 題
周波数が60Hzの電源で駆動されている4極の三相同期電動機(星形結線)があり、端子の相電圧V[V]は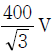
、電機子電流IM[A]は200A、力率1で運転している。1相の同期リアクタンスxs[W]は1.00Ωであり、電機子の巻線抵抗、及び機械損などの損失は無視できるものとして、次の(a)及び(b)の問に答えよ。
(a) 上記の同期電動機のトルクの値[N・m]として最も近いものを、次の(1)～(5)のうちから一つ選べ。
- 12.3
- 368
- 735
- 1270
- 1470
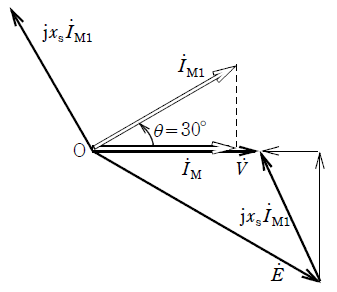
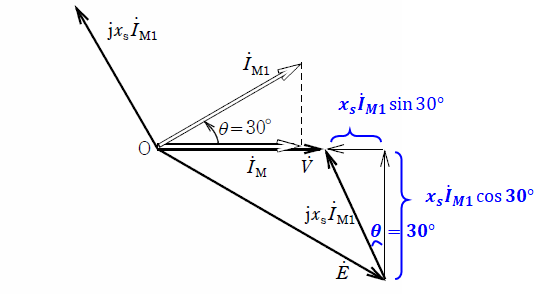
(b) 上記の同期電動機の端子電圧及び出力を一定にしたまま界磁電流を増やしたところ、電機子電流がIM1[A]に変化し、力率cosθが
(θ=30°)の進み負荷となった。出力が一定なので入力電力は変わらない。図はこのときの状態を説明するための1相の概略のベクトル図である。
このときの1相の誘導起電力E[V]として、最も近いEの値を次の(1)～(5)のうちから一つ選べ。
- 374
- 387
- 400
- 446
- 475
解 説
(a)
ここでは同期電動機のトルクの式と出力の式を公式として覚えておくことが重要です。まずは以下の3式を確認してください(覚えていない場合はぜひ押さえておいてください)。
- T：トルク[N・m]
- P：出力[W]
- ω：角速度[rad/s]
- Eo：内部誘導起電力[V] (相電圧実効値)(この問題ではE)
- V：電機子端子電圧[V] (相電圧実効値)
- X：同期リアクタンス[Ω] (この問題ではxs)
- δ：EoとVとの位相角[rad]
- Ns：同期速度[min-1]
- p：磁極の数[極]
- f：周波数[Hz]
このうち、2つ目の式のEとsinδは、Esinδ=xsIMと変換できます。これは知識として覚えるというよりは、以下の図を描いて考えることができます。
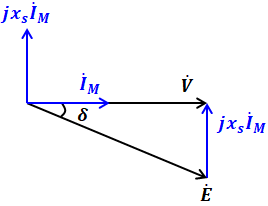
上図は、問題文にある図(これは(b)用ですが)を参考に、力率が1なので、θ=0°として描いています。この図より、Esinδ=xsIMが成り立つことがわかります。
以上の4式を使えば、以下の通り計算することでトルクTの値が求められます。
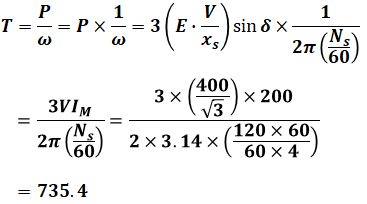
(b)
Eを答える問題ですが、問題文で与えられた数値を下図のように書き込むと、三平方の定理でEを出すことができます。
ここで、IM1はこれも上図から、
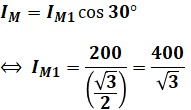
とわかるので、先ほどの式に代入すると、
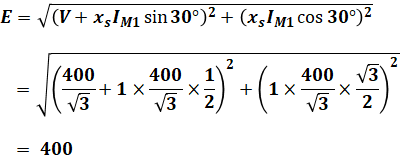
のように答えを出すことができます。
コメント