問 題
一般的な三相かご形誘導電動機がある。
出力が大きい定格運転条件では、誘導機の等価回路の電流は、「二次電流≫励磁電流」であるから、励磁回路を省略しても特性をほぼ表現できる。
さらに、「二次抵抗による電圧降下≫その他の電圧降下」となるので、一次抵抗と漏れリアクタンスを省略しても、おおよその特性を検討できる。
このような電動機でトルク一定負荷の場合に、電流100Aの定格運転から電源電圧と周波数を共に10%下げて回転速度を少し下げた。
このときの電動機の電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 80
- 90
- 100
- 110
- 120
解 説
まず、以下に三相誘導電動機のL形等価回路を示します(三相誘導電動機の等価回路にはL形等価回路とT形等価回路がありますが、ここでは計算の簡単なL形を使います。T形については問6の解説を参照してください)。
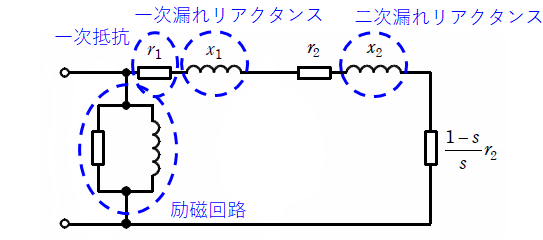
上図のうち、問題文より励磁回路と一次抵抗、漏れリアクタンス(一次・二次とも)を省略できるので、この等価回路は下図左側のように描き換えることができ、2つの抵抗を合成すると下図右側のようになります(この問題では敢えて下図左側を右側に直す必要はありませんが、図を単純化したほうがわかりやすいのでそうしています)。
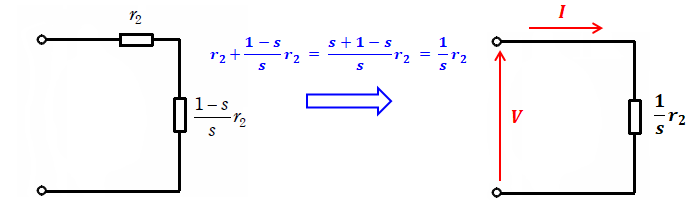
この抵抗が1つだけの単純な等価回路において、電圧Vと周波数fが10%下がったら、電流Iはどうなるか、というのがこの問題のテーマです。
まず、この誘導電動機の二次入力P[W]について考えます。なぜ突然Pなのかというと、Pはfを使った式とVを使った式の両方で表すことができるからです。
先にPとfをつなぐ式を紹介すると、二次入力Pは角速度ω(=2πf)とトルクTとの積になります。これは重要公式として押さえてください。
![]()
問題文よりTは一定なので、fを10%下げた後の二次入力P’は0.9Pとなることがわかります。
続いて、PとVをつなぐ式について、等価回路には抵抗が1つあるのみなので、PはVとIの積です。
![]()
ここで、電圧Vを10%下げたときの電圧V’は0.9Vとなり、周波数fを10%下げたら上記の通りP’が0.9Pとなるので、そのときの電流I’は次のように計算することができます。
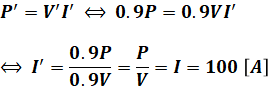
以上の計算から、I’は結局、もともとのI=100[A]となることがわかります。
よって、正解は(3)です。

コメント