問 題
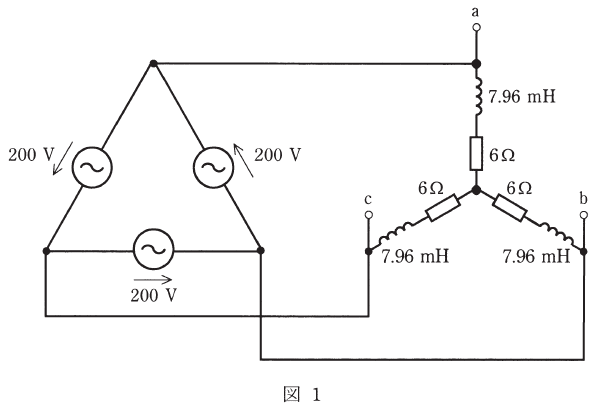
図1のように、周波数50[Hz]、電圧200[V]の対称三相交流電源に、インダクタンス7.96[mH]のコイルと6[Ω]の抵抗からなる平衡三相負荷を接続した交流回路がある。次の(a)及び(b)の問に答えよ。
(a) 図1において、三相負荷が消費する有効電力P[W]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 1890
- 3280
- 4020
- 5680
- 9840
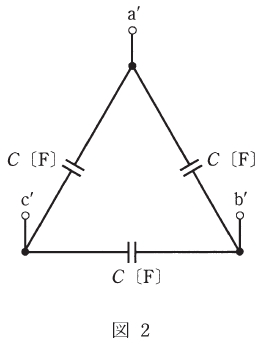
(b) 図2のように、静電容量C[F]のコンデンサをΔ結線し、その端子a’、b’及びc’をそれぞれ図1の端子a、b及びcに接続した。その結果、三相交流電源からみた負荷の力率が1になった。静電容量C[F]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 6.28×10-5
- 8.88×10-5
- 1.08×10-4
- 1.26×10-4
- 1.88×10-4
解 説
(a)
まず電源側(図1の左側)をΔ結線からY結線に変換して、Y-Y結線にした上で1相分の等価回路を抜き出して描くと、計算しやすくなります。その等価回路は以下のように描けます。

上図のうち、電圧が200/√3[V]なのは、Δ結線→Y結線の変換により、電圧が√3分の1になるためです。また、コイルのインダクタンスが7.96[mH]なので、そのリアクタンスXL[Ω]は、
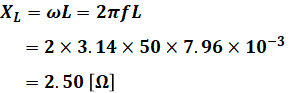
となります。よって、抵抗とリアクタンスを合わせたインピーダンス[Ω]は、
![]()
となるので、上図の回路を流れる電流I[A]は、以下のように計算できます。
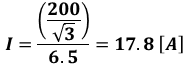
以上より、求める有効電力P[W]は、この回路の電力を3つ分(3相分)なので、
![]()
となります。よって、最も近い(4)が正解となります。
ちなみに、計算結果と選択肢の答えが少しずれてしまっているのは、電流I[A]を17.8として計算しているためです。ここで、平方根の計算や四捨五入などをせず、最後の電力の計算のところでまとめて計算すれば、ちゃんと5680[W]になります(今回は見た目の上で煩雑な計算式にならないよう、電流はそれ単独で計算しました)。
(b)
(b)でも(a)と同様、追加する図2のΔ結線をY結線に直してから、1相分の等価回路について考えるとわかりやすいと思います。その等価回路は以下のように描くことができます(XLは(a)での計算結果を使います)。
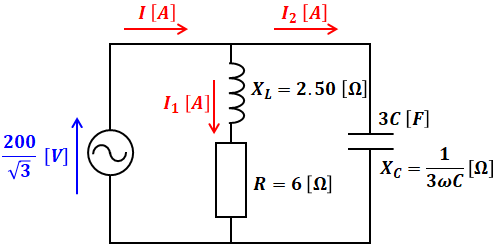
ここで、図中右側のコンデンサの静電容量を3C[F]としているのは、Δ結線→Y結線の変換により、静電容量が3倍になるためです。
設問では「三相交流電源からみた負荷の力率が1」とあるので、電源を流れる電流Iの位相が、電圧の位相と一致すればよく、つまりは電流Iの虚数のところを0にする必要があります。
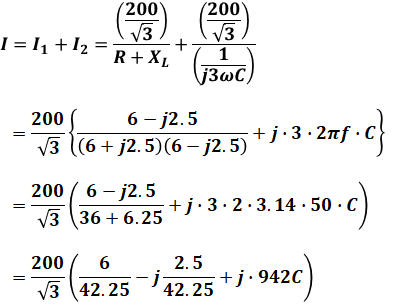
より、虚数を0にするには、次のように計算します。
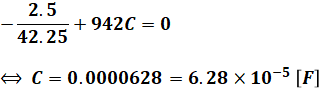

コメント