問 題
出力600[kW]の太陽電池発電所を設置したショッピングセンターがある。ある日の太陽電池発電所の発電の状況とこのショッピングセンターにおける電力消費は図に示すとおりであった。
すなわち、発電所の出力は朝の6時から12時まで直線的に増大し、その後は夕方18時まで直線的に下降した。
また、消費電力は深夜0時から朝の10時までは100[kW]、10時から17時までは300[kW]、17時から21時までは400[kW]、21時から24時は100[kW]であった。
このショッピングセンターは自然エネルギーの活用を推進しており太陽電池発電所の発電電力は自家消費しているが、その発電電力が消費電力を上回って余剰を生じたときは電力系統に送電している。
次の(a)及び(b)の問に答えよ。

(a) この日、太陽電池発電所から電力系統に送電した電力量[kW・h]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 900
- 1300
- 1500
- 2200
- 3600
(b) この日、ショッピングセンターで消費した電力量に対して太陽電池発電所が発電した電力量により自給した比率[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 35
- 38
- 46
- 52
- 58
解 説
まず、解説のために問題文の図に書き込みをしたものを下図に示します。
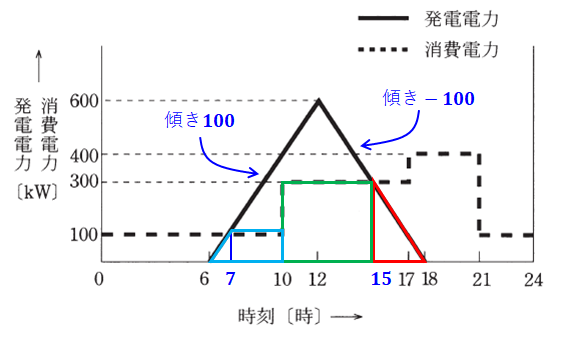
上図中央の三角形の傾きは、図示の通り100と-100になります。その理由は、三角形の左斜辺に関しては、横軸6時間分(6~12)で縦軸が600[kW]ほど上がっているため、傾きは100になります。また、三角形の右斜辺に関しては、横軸6時間分(12~18)で縦軸が600[kW]ほど下がっているため、傾きは-100になります。
よって、そのことから求めたのが、横軸に青字で「7」と「15」と示した時刻です。
(a)
電力系統に送電した電力量を問うているので、総発電量から自家消費した分を引けばよいことになります。つまり、上図中央の三角形(=総発電量)から、水色の台形+緑色の長方形+赤色の三角形の合計(=自家消費)を引いた値です。
- (中央の三角形)=12×600÷2=3600 [kW]
- (水色の台形)=(3+4)×100÷2=350 [kW]
- (緑色の長方形)=5×300=1500 [kW]
- (赤色の三角形)=3×300÷2=450 [kW]
より、
- (電力系統に送電した電力量)=3600-(350+1500+450)=1300 [kW]
となるので、正解は(2)です。
(b)
ショッピングセンターで消費した電力量を求める必要がありますが、図中の破線の下側の面積が該当します。そのうち、自給した電力(=自家消費)の割合を問うていますが、そちらはすでに求めた水色+緑色+赤色のことです。
破線の下側の面積を計算するにあたり、100[kW]が13時間(0~10と21~24)、300[kW]が7時間(10~17)、400[kW]が4時間(17~21)です。よって、
- (消費電力量)=100×13+300×7+400×4=5000 [kW]
になります。また、上記より自給した電力(=水色+緑色+赤色)は2300[kW](=350+1500+450)なので、その比率は、
![]()
となるので、正解は(3)です。

コメント