問 題
図のように、三つの平行平板コンデンサを直並列に接続した回路がある。ここで、それぞれのコンデンサの極板の形状及び面積は同じであり、極板間には同一の誘電体が満たされている。なお、コンデンサの初期電荷は零とし、端効果は無視できるものとする。
いま、端子a-b間に直流電圧300[V]を加えた。このとき、次の(a)及び(b)の問に答えよ。
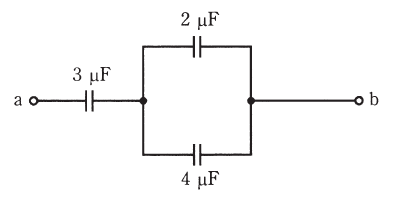
(a) 静電容量が4[μF]のコンデンサに蓄えられる電荷Q[C]の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
- 1.2×10-4
- 2×10-4
- 2.4×10-4
- 3×10-4
- 4×10-4
(b) 静電容量が3[μF]のコンデンサの極板間の電界の強さは、4[μF]のコンデンサの極板間の電界の強さの何倍か。倍率として、正しいものを次の(1)~(5)のうちから一つ選べ。
- 3/4
- 1.0
- 4/3
- 3/2
- 2.0
解 説
(a)
まずは直流電圧300[V]とそれぞれのコンデンサの静電容量から、各コンデンサにかかる電圧を考えます。並列に並んでいるコンデンサの静電容量を合成する際は、そのまま和で表すことができるので、右側のコンデンサを合成すると、問題文の図は以下のように描き換えることができます。
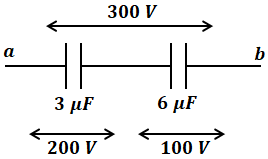
ここで、電荷Qと静電容量Cと電圧Vの関係は
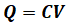
となりますが、直列に並んだコンデンサは電荷が等しいので、静電容量が3:6=1:2であれば、電圧は逆に2:1になります。よって、電圧は上図に書き込んであるように、左側が200[V]、右側が100[V]とわかります。
よって、求めるべき電荷Qは静電容量C=4[μF]、電圧V=100[V]から、次のように計算できます。
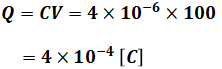
(b)
電界の強さEは電圧Vと板間距離dから求められます。
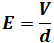
しかし、この問題では板間距離に関する情報が与えられていないため、このままでは比較ができません。問題文で問われているのは、静電容量が3[μF]と4[μF]のコンデンサの電界の強さを比較することなので、板間距離と静電容量との関係がわかればよいということになります。よって、静電容量を求めるための以下の式が使えます。
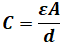
- C:静電容量[F]
- ε:誘電率[F/m]
- A:板の面積[m2]
- d:板間距離[m]
上式2つをまとめると、次のようになります。
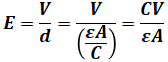
ここで、問題文より「コンデンサの極板面積は同じ」、「同一の誘電体」とあるので、上式のεとAはどのコンデンサでも同じあり、比較対象は分子のCVということになります。
静電容量が3[μF]のコンデンサの電圧は、(a)で求めたように200[V]です。よって、こちらのCVは3×200=600となります(比の問題なので、μFをわざわざ10の-6乗してFに直したりはしていません)。
一方、静電容量が4[μF]のコンデンサの電圧も(a)の結果が使え、こちらは100[V]です。よって、CVは4×100=400となります。
以上から、前者の電界の強さは、後者と比べると、
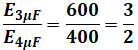
と計算することができます。

コメント