問 題
極板A-B間が誘電率ε0[F/m]の空気で満たされている平行平板コンデンサの空気ギャップ長をd[m]、静電容量をC0[F]とし、極板間の直流電圧をV0[V]とする。極板と同じ形状と面積を持ち、厚さがd/4[m]、誘電率ε1[F/m]の固体誘電体(ε1>ε0)を図に示す位置P-Q間に極板と平行に挿入すると、コンデンサ内の電位分布は変化し、静電容量はC1[F]に変化した。
このとき、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、空気の誘電率をε0、コンデンサの端効果は無視できるものとし、直流電圧V0[V]は一定とする。
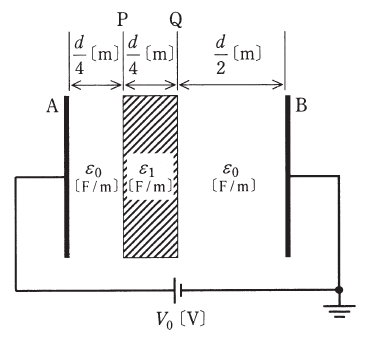
- 位置Pの電位は、固体誘電体を挿入する前の値よりも低下する。
- 位置Qの電位は、固体誘電体を挿入する前の値よりも上昇する。
- 静電容量C1[F]は、C0[F]よりも大きくなる。
- 固体誘電体を導体に変えた場合、位置Pの電位は固体誘電体又は導体を挿入する前の値よりも上昇する。
- 固体誘電体を導体に変えた場合の静電容量C2[F]は、C0[F]よりも大きくなる。
解 説
誘電体は直流回路においては絶縁体として働き、電荷を流れにくくします。ここで、電荷を流れにくくするということは溜めやすくするともいえるので、静電容量は増えます。そして、コンデンサに蓄えられる電荷の量は変わらないので、静電容量が増える分、そこでの電圧幅は小さくなります。
以上のことを式で説明すると、次のようになります。
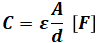
- C:静電容量[F]
- ε:誘電率[F/m]
- A:板の面積[m2]
- d:板間距離[m]
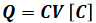
- Q:電荷[C]
- V:電圧[V]
上式の1つ目を見てもわかるように、誘電体を挿入することでε0がε1に変化すると(ε1>ε0)、Cは大きくなります。よって、まずは選択肢(3)の記述が正しいことがこの時点で決まります。
また、少し話がずれますが、選択肢(5)は誘電体を入れていた部分を導体に変えるということなので、もともとはAB間でd[m]あった板間距離が、d/4[m]分だけ短くなったことになるので、上式1つ目の式でdが小さくなるとCは大きくなることがわかるので、選択肢(5)も正しい記述と判断できます。
ここで話を戻します(つまり、初期状態から誘電体を挿入したことにより、Cが大きくなったという状態です)。2つ目の式においてQは不変とすると、Cが大きくなればVは小さくなることがわかります。よって、この区間(PQ間)のVは、誘導体を挿入することで小さくなります。
これを問題の通り各パラメータが記号のままで考えるよりも、数値化して考えたほうがわかりやすいと思います。ここでは具体的に、V0=100[V]とすると、A、P、Q、Bの各点の電圧は次のように描くことができます。
- 誘電体挿入前
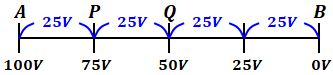
- 誘電体挿入後
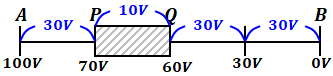
各数値は適当ですが、ポイントはPQ間の電圧差が小さくなることで、ほかの区間の電圧差が大きくなるということです(直流電源をつないでいる以上、AB間が100[V]であることは固定であるため)。
よって、この図において位置Pの電位は75[V]から70[V]に低下したため、選択肢(1)は正しいといえます。また、位置Qの電位は50[V]から60[V]に上昇しているため、選択肢(2)も正しいことがわかります。
そして、残る選択肢(4)では誘電体のところが導体となるため、上図に合わせて描くと次の図のようになります。
- 導体に変更した場合
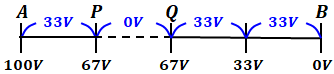
このように、PQ間はコンデンサではなく導体なので、電流がそのまま流れて電位差を生じません(0[V]です)。よって、残るAP間とQB間で、100[V]分の電圧差が距離に応じて均等配分されます。つまり、この例では位置Pの電位は67[V]となり、最初の75[V]よりも誘電体挿入後の70[V]よりも低いため、選択肢(4)の記述が誤りであることがわかります。

コメント