問 題
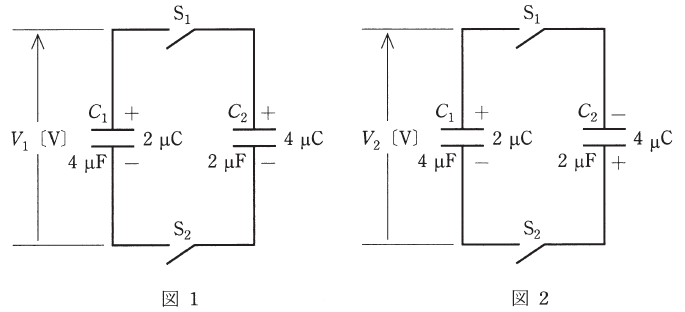
図1及び図2のように、静電容量がそれぞれ4[μF]と2[μF]のコンデンサC1及びC2、スイッチS1及びS2からなる回路がある。コンデンサC1とC2には、それぞれ2[μC]と4[μC]の電荷が図のような極性で蓄えられている。
この状態から両図ともスイッチS1及びS2を閉じたとき、図1のコンデンサC1の端子電圧をV1[V]、図2のコンデンサC1の端子電圧をV2[V]とすると、電圧比![]() の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
- 1/3
- 1
- 3
- 6
- 9
解 説
まずは図1のほうから考えます。2つのコンデンサが並列に並んでいるときは、その合成は単純な和として表すことができます(下図左側参照)。ちなみに、直列に並んでいる場合は逆数にしてから足して、また逆数に戻す必要があります。抵抗の直列や並列のときと、その計算方法が反対になります。よって、コンデンサの静電容量CはC1とC2の和で、4+2=6[μF]です。
また、電荷は2つのコンデンサのどちらも上側が+で下側が-と向きがそろっているため、これも合成の際には単純に足すことができます(もし向きが反対なら、引き算をすることになります)。よって、電荷Qは、2+4=6[μC]となります。
以上から、図1の端子電圧V1は、
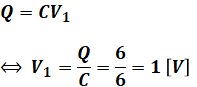
となります(CもQもμのオーダーなので、μ同士を約分して計算しています)。
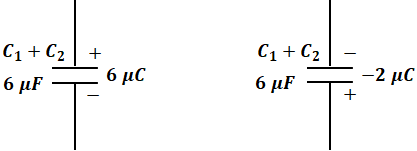
続いて、図2のほうを考えます。こちらも図1と同様に考えると、上図右側のようになります。
注意すべき点は、2つのコンデンサが接続されている側(上側同士or下側同士)での電荷の正負が異なるので、電荷の合成の際には単純な和になるのではなく、正負の記号を含めた和(つまり、差)になることです。よって、電荷Q’は、2-4=-2[μC]となります(回路の上側が-2[μC]で下側が+2[μC]になります)。
一方、コンデンサの静電容量C’は「容量(電荷が入る入れものの大きさ)」なので、正負などはなく、図1と同じように考えることができるので、4+2=6[μF]となります。
以上から、図2の端子電圧V2は、
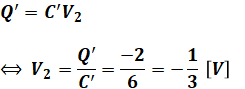
となります。
よって、求める答えは以下のように計算することができます。
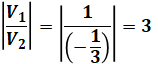

コメント