問 題
単相変圧器があり、二次側を開放して電流を流さない場合の二次電圧の大きさを100[%]とする。二次側にリアクトルを接続して力率0の電流を流した場合、二次電圧は5[%]下がって95[%]であった。二次側に抵抗器を接続して、前述と同じ大きさの力率1の電流を流した場合、二次電圧は2[%]下がって98[%]であった。
一次巻線抵抗と一次換算した二次巻線抵抗との和は10[Ω]である。鉄損及び励磁電流は小さく、無視できるものとする。
ベクトル図を用いた電圧変動率の計算によく用いられる近似計算を利用して、一次漏れリアクタンスと一次換算した二次漏れリアクタンスとの和[Ω]の値を求めた。その値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 5
- 10
- 15
- 20
- 25
解 説
変圧器の電圧変動率については、その定義はともかく、電験三種の試験では以下の近似式を使います(この手の問題では、おそらく毎回、問題文に近似計算を行う旨が記載されます)。そのため、以下の式を公式として覚えておくと良いと思います。
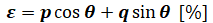
- ε:電圧変動率[%]
- p:百分率抵抗降下(パーセント抵抗)[%]
- q:百分率リアクタンス降下(パーセントリアクタンス)[%]
- cosθ:力率
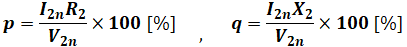
- I2n:定格運転時の二次電流[A]
- R2:二次側に換算した等価回路の抵抗[Ω] (R2=r1/α2+r2)
- X2:二次側に換算した等価回路のリアクタンス[Ω] (X2=x1/α2+x2)
- V2n:定格運転時の二次電圧[V]
今回の場合は、問題文の2文目では百分率リアクタンス降下q[%]のことを、3文目では百分率抵抗降下p[%]のことを指しているので、上記に示した公式のうち、下の式だけを使います。
まずは百分率抵抗降下p[%]について、公式に問題文で与えられている数値を代入します。
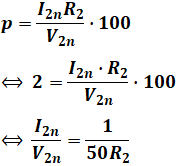
続いて、百分率抵抗リアクタンスq[%]についても同様ですが、上記で求めた値も一緒に代入することで、リアクタンスX2[Ω]を、R2[Ω]を用いた式として表すことができます。
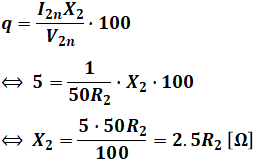
ここで、上式は二次側換算した抵抗やリアクタンスを含む式となっていますが、この問題で求めたいのは一次側換算したリアクタンスであることに注意してください。
とはいえ、一次側換算でも二次側換算でも抵抗とリアクタンスの比は変わらないので、「一次巻線抵抗と一次換算した二次巻線抵抗との和」をR1[Ω]、「一次漏れリアクタンスと一次換算した二次漏れリアクタンスとの和」をX1[Ω]とすると、X1は次のような計算によって求めることができます。
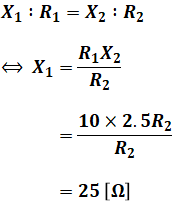

コメント