問 題
次の文章は、水力発電の理論式に関する記述である。
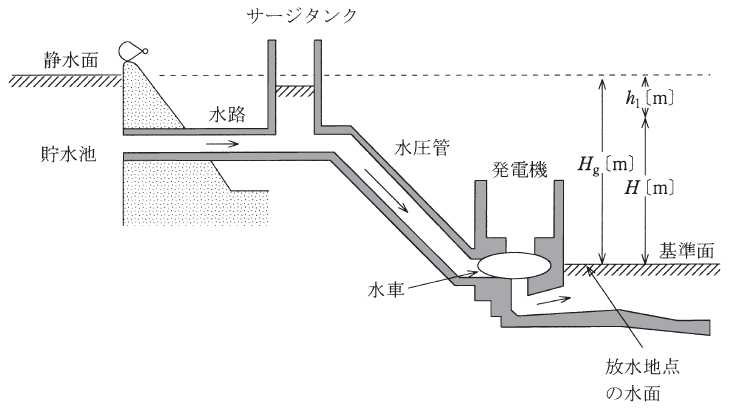
図に示すように、放水地点の水面を基準面とすれば、基準面から貯水池の静水面までの高さHg[m]を一般に( ア )という。また、水路や水圧管の壁と水との摩擦によるエネルギー損失に相当する高さh1[m]を( イ )という。さらに、Hgとh1の差H=Hg-h1を一般に( ウ )という。
いま、Q[m3/s]の水が水車に流れ込み、水車の効率をηwとすれば、水車出力をPwは( エ )になる。さらに、発電機の効率をηgとすれば、発電機出力Pは( オ )になる。ただし、重力加速度は9.8[m/s2]とする。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

解 説
( ア )ではHgのことを問われていますが、基準面から静水面までの高さのことを「総落差」といいます。ただし、この分の位置エネルギーが全て発電に使えるわけではなく、実際にはh1の分だけロスが出てしまいます。
このh1のことを「損失水頭」といい、実質的に発電に回せるエネルギー分の落差を「有効落差」といいます。よって、( イ )と( ウ )も決まり、この時点で選択肢(3)が正解だとわかります。
一応、確認のため、( エ )と( オ )についても見ていきます。
水車の出力は、理論的には位置エネルギーがそのまま運動エネルギーに変換されるので、理想としては
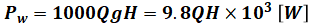
となります(Qの係数が1000となっているのは、Q[m3]の水はQ[t]分の重さがあり、つまりは1000Q[kg]だからです)。しかし、実際には水車の効率がたとえば0.8(80%)だったら、理想の0.8倍しなければいけません。よって、水車の出力は以下のようになります。
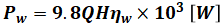
同様に、発電機の効率がたとえば0.95(95%)であれば、水車の出力にさらに0.95を掛けたものが発電機出力になります。
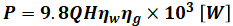
以上より、( エ )と( オ )も選択肢(3)の通りであることを確認できました。
よって、正解は(3)となります。

コメント