単相3線式配電線路の計算問題として出題されるのは、
- 変圧器の一次側を流れる電流の値 [A]
- 回路図中に流れる未知の電流値 [A]
- 回路図中のある2点の電圧差 [V]
などのパターンが挙げられます。
この項では、これらの計算方法をそれぞれ紹介していきます。
変圧器の一次側を流れる電流の値
まずは以下の回路図から、変圧器の一次側を流れる電流の値を求めます。
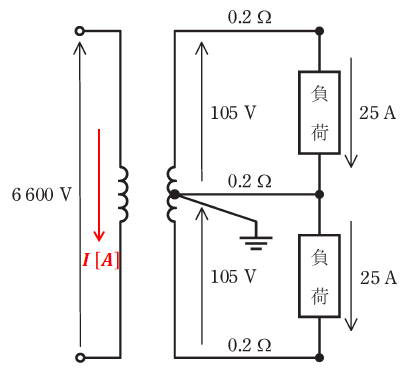
上図において、変圧器の一次側と二次側の電力は同じです。よって、一次側の電圧がわかっていて、二次側の電圧と電流がわかっていれば、次のように一次側の電流I [mA]を計算することができます。
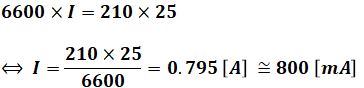
回路図中に流れる未知の電流値
続いて、以下に示す回路図において、未知の電流I[A]を求める方法について解説します。今回は、回路図中に流れる未知の電流値が、太陽光発電設備を流れる電流I[A]のところだとします。
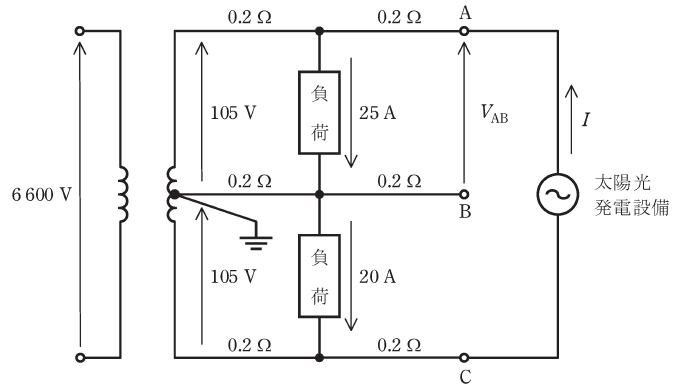
条件:
- 図示していないインピーダンスは無視できる
- 図示してあるインピーダンスはすべて抵抗である
- 負荷や太陽光発電設備の力率は1とする
このとき、上図のVABは107[V]とします。これは既知の値として問題文で与えられていると考えてください。
上記の条件を回路図に書き込むと、以下のようになります。
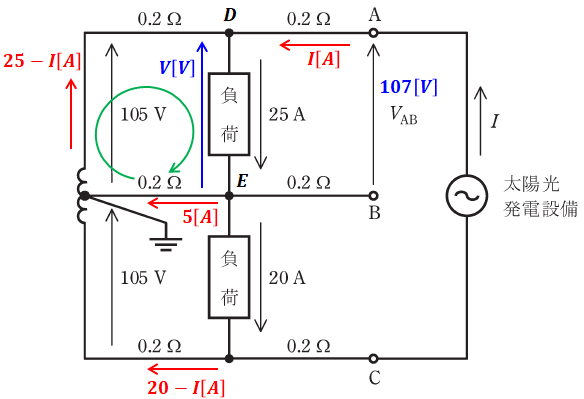
上図において、DE間の電圧V[V]は、AB間の電圧とAD間の電流と抵抗から、次のように表すことができます。
![]()
よって、上図の緑矢印で示した閉回路でキルヒホッフの法則を用いると、以下の等式が成り立ちます。
![]()
これをIについて解くと、次のようになります。
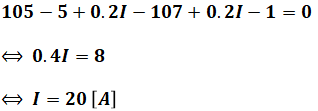
太陽光発電設備を流れる電流Iは20[A]と算出することができます。
回路図中のある2点の電圧差
先ほどはVAB[V]を使ってI[A]を求めましたが、今度は反対にIが既知の値(20[A])であり、VAB[V]が未知の値という想定で、2点の電圧差VAB[V]の算出の仕方を考えてみます。
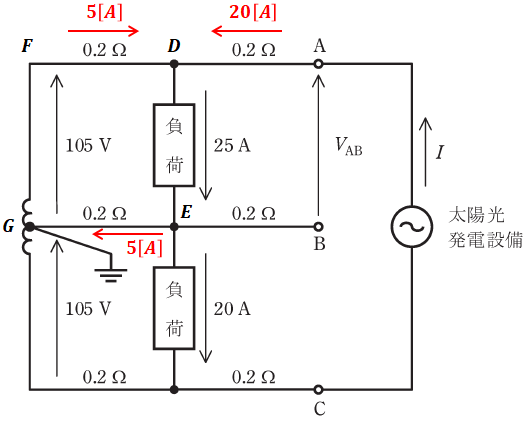
上記において、最終的に求めたいのは点Aと点Bの電圧差VAB[V]ですが、最初の段階でわかっているのは、点Fと点Gの電圧差が105[V]ということです。
点Fを105[V]、点Gを0[V]としておくと、オームの法則を使うと、
- 点D:105-5×0.2=104 [V]
- 点E:0+5×0.2=1 [V]
となり、さらに、
- 点A:104+20×0.2=108 [V]
- 点B:点Eと同じなので、1 [V]
となります。
点Bと点Eの間には電流が流れていない(回路になっていない)ため、この2点の電圧差はありません。以上より、点Aと点Bの電圧差VAB[V]は、
108-1=107 [V]
と計算できます。

コメント