水力発電所の水源が河川から直接取るような水路式であれば、有効落差が上下することはあまりありません。雨が多く降れば流量は増え、発電量も増えます。雨が降らなければ流量が減り、発電量も少なくなります。この際、河川の中の水の水位が大きく変わることはないので、有効落差は大体一定しています。
一方、ダム式の場合、雨が多く降ればダムの水位は高くなりますし、ピーク発電をおこなった後だと水位は下がります。このようにダム式のときは有効落差が上下することがよくあります。
さて、有効落差が変化すると、流量や水車の回転速度、出力がどのように変化するのか、というのが本項のテーマです。
流量と有効落差の関係式
まず、流量と有効落差の関係は次のとおりです。

- Q1:変化前の流量[m3/s]
- Q2:変化後の流量[m3/s]
- H1:変化前の有効落差[m]
- H2:変化後の有効落差[m]
有効落差が大きくなれば流量も上がり、有効落差が小さくなれば流量も下がる…というのはイメージ通りだと思いますが、それは上式の通り√に比例します。この式は、前項で紹介したベルヌーイの定理を使って導くことができます。
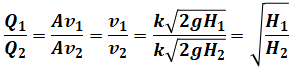
水車の回転速度と有効落差の関係式
次に、水車の回転速度と有効落差の関係を示します。
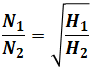
- N1:変化前の回転速度[s-1]
- N2:変化後の回転速度[s-1]
こちらも上記の流量-有効落差の関係と同様です。この式の導出過程は以下のようになります。
まず、ランナ周速u[m/s]は流入速度v[m/s]に比例します。すると、前述の式の一部、
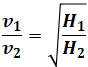
を使うと、
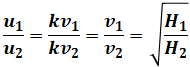
となります。
一方、ランナ周速u[m/s]は回転速度N[s-1]とランナの円周の積でも表せるので、直径をD[m]とすると円周はπD[m]となり、
![]()
が成り立ちます。
以上より、水車の回転速度と有効落差の関係式である以下の式が成り立ちます。
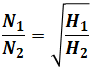
出力と有効落差の関係式
最後に、出力と有効落差の関係は次のようになります。
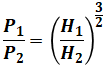
- P1:変化前の出力[kW]
- P2:変化後の出力[kW]
この式の導出過程は次のようになります。

まとめ
導出過程の式が多く入ったので、この項の最後に以上の要点だけをまとめておきます。過程はともかく、結果を知らないと解けない問題もありますので、ぜひこれらの関係式を覚えるようにしてください。

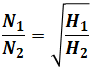
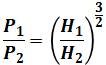

コメント