問 題
受電端電圧が20kVの三相3線式の送電線路において、受電端での電力が2000kW、力率が0.9(遅れ)である場合、この送電線路での抵抗による全電力損失の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、送電線1線当たりの抵抗値は9Ωとし、線路のインダクタンスは無視するものとする。
- 12.3
- 37.0
- 64.2
- 90.0
- 111
正解 (5)
解 説
まずは三相3線式のうち1相と中性線とを結んだ等価回路を以下に示します。
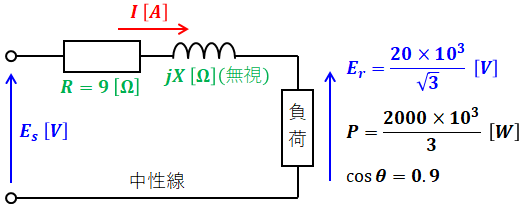
- Es:送電端電圧 [V]
- Er:受電端電圧 [V]
- I:線電流 [A]
- R:抵抗(電線1条あたり) [Ω]
- X:リアクタンス(電線1条あたり) [Ω]
- P:受電端での電力(1相分) [W]
- cosθ:力率
ここでは三相3線式のうち1相を取り出しているので、問題文で与えられている数値から、Erは1/√3倍、Pは1/3倍となります。また、インダクタンスは無視できるので、リアクタンスjX=0です。
上図より、電流Iは次のように計算できます。
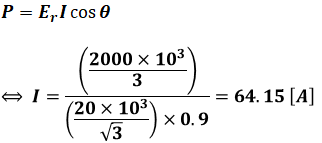
よって、1相あたりの等価回路において、配電線路での抵抗による電力損失Plossは次のように計算できます。
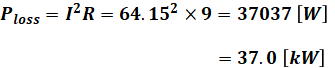
上記は1線分の電力損失なので、これを3倍することで三相3線式配電線路全体の電力損失となります。
![]()
以上から、正解は(5)です。

コメント