本項では、%Z(%インピーダンス)の計算方法について解説をします。
変圧器や送電線を安全に運用するためには、起こりうる事故を予想し、その対策を立てておく必要があります。つまり、送電線のある地点で短絡事故が起こったときには短絡電流が生じますので、それがどのくらいの電流になるのかを計算し、それに耐え得る遮断器を選べばよいわけです。
この際、変圧器の前後では電圧が異なりますし、それに応じて電流も変化します。そのような複雑な条件では計算が難しくなりますので、この計算を簡単化するために、「%Z(%インピーダンス)法」を使います。
%Zとは、全負荷電流下でのインピーダンス降下(IZ)と相電圧(E)の比を百分率で表したものです。これにより、複数地点のインピーダンスを基準電流・基準電圧のインピーダンスに統一できるので、比較や計算がしやすくなります。
![]()
相電圧(E)を線間電圧(V)で表すと、V=√3Eより、
![]()
となります。この2つ目の式はぜひ覚えておいてください。
本項の冒頭で、事故時に流れる電流を計算で求めてそれに対応できる遮断器を選べばよいと書きましたが、最も大きな電流が流れる事故は三相短絡事故なので、このときに流れる「三相短絡電流」を計算すればよいことになります。
三相短絡電流の求め方を説明するために、まずは以下の図をみてください。
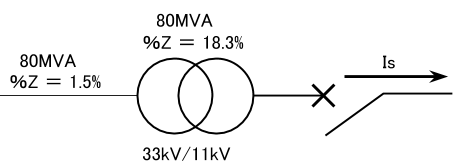
左側に電源、右側に負荷があり、中央の○○が変圧器です。33/11[kV]は変圧前後の電圧を示しています。図には%Zが1.5%と18.3%とありますが、これは80[MV・A]を基準としています。
基準が一致している場合は、直列に並ぶ%Zはそのまま足し算ができます。また、並列に並ぶ場合は各%Zを逆数にしてから足し算をして、その逆数を戻せば合成できます。つまり、電気回路の抵抗の合成と同じ計算方法です。
ちなみに、上図では80[MV・A]と基準が揃っていましたが、実際の出題では異なることもしばしばあります。例えば50[MV・A]基準で%Zが3%のものと、100[MV・A]基準で%Zが2%のものがあれば、両方を100[MV・A]基準に統一するため、前者を100/50×3=6%とします。もしくは両者を50[MV・A]基準に統一して、後者を50/100×2=1%とします。
話を図の計算に戻します。事故点での短絡電流Isを求めるのが目的ですが、その式は以下のようになります。
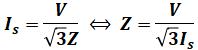
これと、上記の%インピーダンスの式を組み合わせると、
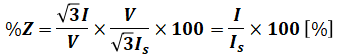
となります。
また、%ZとIは次の式で表されるので、
![]()
![]()
これらを先ほどの式に代入すると、次のように短絡電流Isが求まります。
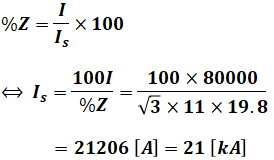
よって、三相短絡電流は21[kA]とわかったので、遮断器はこれより大きい定格遮断電流を有するもの(例えば25[kA])を選べばよい、ということになります。選択問題なので、定格遮断電流を超える中で最も小さい数字を選んでください。
以上が%Zについての説明ですが、ここで少し整理をします。
最初に%Zは
![]()
と書きましたが、以上の説明から、次のような表し方もできることになります。
![]()
ここでIは全負荷電流(定格電流)、Isは短絡電流です。つまり、%Zは全負荷電流(定格電流)と短絡電流の比で表されます。
両方の式を覚えていると便利ですが、一方からもう一方を求めることもできるので、少なくともどちらかを理解していれば大丈夫です。

コメント