問 題
熱の伝わり方について、次の(a)及び(b)の問に答えよ。
(a) ( ア )は、熱媒体を必要とせず、真空中でも熱を伝達する。高温側で温度T2[K]の面S2[m2]と、低温側で温度T1[K]の面S1[m2]が向かい合う場合の熱流Φ[W]は、S2F21σ(( イ ))で与えられる。
ただし、F21は、( ウ )である。また、σ[W/(m2・K4)]は、( エ )定数である。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
- ア イ ウ エ
- 熱伝導 T22-T12 形状係数 プランク
- 熱放射 T22-T12 形態係数 ステファン・ボルツマン
- 熱放射 T24-T14 形態係数 ステファン・ボルツマン
- 熱伝導 T24-T14 形状係数 プランク
- 熱伝導 T24-T14 形状係数 ステファン・ボルツマン
(b) 下面温度が350K、上面温度が270Kに保たれている直径1m、高さ0.1mの円柱がある。伝導によって円柱の高さ方向に流れる熱流Φの値[W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、円柱の熱伝導率は0.26W/(m・K)とする。また、円柱側面からのその他の熱の伝達及び損失はないものとする。
- 3
- 39
- 163
- 653
- 2420
解 説
(a)
本問は、熱の伝わり方(伝熱)の3つのパターン「伝導、対流、放射」のうち「放射」の出題です。伝導は固体の中での熱の移動、対流は流体(液体や気体)の流れを伴う熱の移動であるのに対し、放射は電磁波による熱の移動で、熱媒体を必要とせず真空中でも熱を伝達します。
よって、( ア )には「熱放射」が入ります。
熱放射のエネルギーは、温度の4乗に比例します。これは知識として押さえておきたい重要事項です。
今回のように2つの面が向かい合う場合には、そのエネルギー差が熱流Φ[W]となるので、( イ )には「T24-T14」が入ります。
温度の高いほうから低いほうへと流れますが、そのエネルギー(熱流Φ[W])は温度の4乗に比例します。
( ウ )はややマイナーな知識ですが、これがわからなくてもほかの3つが正しく答えられれば選択肢は1つに絞られるので、そこまで気にしなくてもいいと思います。
この式において、F21は面S1、面S2の大きさ、形状、相対位置などの幾何学的な関係で決まる値であり、これを形態係数といいます。よって、( ウ )は「形態係数」となります。
( エ )に関して、熱流は温度の4乗の差に比例するというこの式で用いられる比例定数σは、ステファン・ボルツマン定数です。これはときどき出題される知識なので、ぜひ押さえておきたいところです。よって、( エ )は「ステファン・ボルツマン」となります。
ちなみに、選択肢にあるプランク定数は、放射エネルギーは振動数に比例する、という法則の比例定数です。
![]()
- E:光子のエネルギー[J]
- h:プランク定数[J/s]
- v:振動数[Hz]=[s-1]
以上から、( ア )は「熱放射」、( イ )は「T24-T14」、( ウ )は「形態係数」、( エ )は「ステファン・ボルツマン」となるので、正解は(3)です。
(b)
熱流Φの式は一見すると問題文で与えられているように思えますが、F21やσの値が不明なので、計算を進めることができません。よって、ここでは別のアプローチが必要となります。
(b)の設問で与えられている条件を図に示すと、以下のようになります。
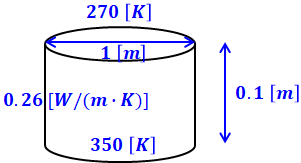
上図を見てもわかるように、円柱が太い(面の面積が大きい)ほど熱が流れやすくなるので、熱流は大きくなります。また、円柱が長いほど熱は流れにくくなるので、熱流は小さくなります。さらに、上面と下面の温度差が大きければ熱は流れやすく、温度差が小さければ熱が流れにくいということもイメージしやすいと思います。
よって、熱流は「面の面積」と「上面と下面の温度差」に比例し、「距離」に反比例します。
単位に注意にしつつ、以上のことを式にすると、以下のように計算できます。
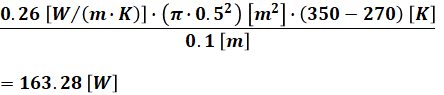
以上から、正解は(3)です。

コメント