問 題
発振回路について、次の(a)及び(b)の問に答えよ。
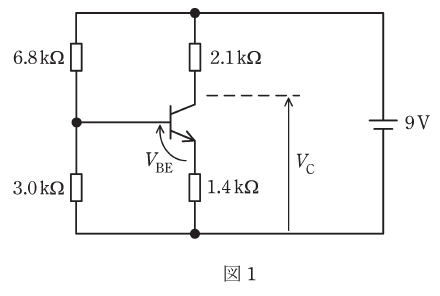
(a) 図1は、ある発振回路のコンデンサを開放し、同時にコイルを短絡した、直流分を求めるための回路図である。図中の電圧VC[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、図中のVBE並びにエミッタ接地トランジスタの直流電流増幅率hFEをそれぞれVBE=0.6V、hFE=100とする。
- 3
- 4
- 5
- 6
- 7
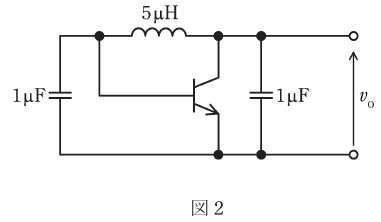
(b) 図2は、ある発振回路のトランジスタに接続されている、電極間のリアクタンスを示している。ただし、バイアス回路は省略している。
この回路が発振するとき、発振周波数f0[kHz]はどの程度の大きさになるか、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、発振周波数は、図に示されている素子の値のみにより定まるとしてよい。
- 0.1
- 1
- 10
- 100
- 1000
解 説
(a)
問われているのは電圧VC[V]です。これを求めるために、まずは下図のようにベース電流をIB[mA]、コレクタ電流をIC[mA]、エミッタ電流をIE[mA]、3.0[kΩ]の抵抗の端子間電圧をVB[V]と表します。ちなみに、電流の単位を[mA]にしているのは、抵抗の単位[kΩ]とバランスを取るためです。
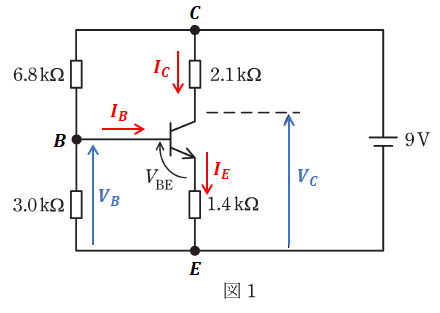
上図より、求めたいVCは、回路図の右半分を使って次のような式で表すことができます。
![]()
よって、ICがわかればVCを求めることができそうです。ここで、問題文よりエミッタ接地トランジスタの直流電流増幅率hFE=100とあるので、下式が成り立ちます。
![]()
(2)式から、今度はIBの値を知る必要が出てきました。そこで、上図の回路図の点Bと点Eの間の電圧に注目します。すると、以下の等式が成り立ちます。
![]()
(3)式のうち、VBは下式によって具体的に計算することができます。
![]()
これは、回路図右側の電源が9[V]であるため、左側に直列に並んでいる2つの抵抗の端子間電圧も9[V]となることから、抵抗比の計算によってVBを求めています。
続いて、(3)式のうち、VBEは問題文で0.6[V]と明記されています。
![]()
そして、(3)式のうち、IEはIBとICの和なので、(2)式も合わせて考えると次のようになります。
![]()
(4)式、(5)式、(6)式を(3)式に代入すると、
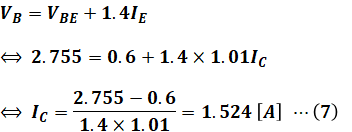
となり、これを(1)式に代入すると、求めたいVCを算出することができます。
![]()
よって、選択肢の中で最も近いのは(4)の「6」なので、正解は(4)です。
(b)
(b)はハイレベルな内容となっていて、難易度の高さや出題頻度の低さの割に点数はほかと同様5点なので、個人的にはこの問題は捨て問題としてしまっても構わないと思います。
ただし、その場合でも(a)は重要事項かつ頻出なので、(a)の解法はきちんと身につけておくことをおすすめします。

上図のトランジスタにおいて、ベース-エミッタ間とコレクタ-エミッタ間のそれぞれにコンデンサが、ベース-コレクタ間にコイルが接続されているような発振回路のことを、コルピッツ発振回路といいます。問題の図2はまさにこの形をしています。
コルピッツ発振回路が発振するとき、全てのコンデンサのリアクタンス(1/jωC)とコイルのリアクタンス(jωL)の和が0になります。今回は、コンデンサ2つが各1[μF]でコイルが5[μH]なので、以下の等式が成り立ちます。
![]()
上式の全ての項にjω(1×10-6)を掛けて、以下のように計算を進めます。
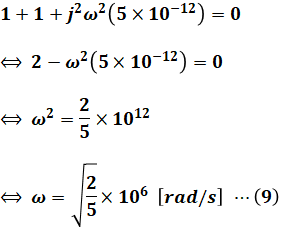
ここで、ω=2πfより、(9)式から以下のように計算することで、発振周波数f0[kHz]を求めることができます。
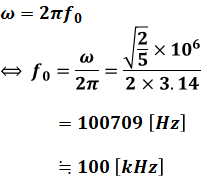
よって、正解は(4)となります。

コメント