問 題
図のように、電源E[V]、負荷抵抗R[Ω]、内部抵抗Rv[Ω]の電圧計及び内部抵抗Ra[Ω]の電流計を接続した回路がある。
この回路において、電圧計及び電流計の指示値がそれぞれV1[V]、I1[A]であるとき、次の(a)及び(b)の問に答えよ。ただし、電圧計と電流計の指示値の積を負荷抵抗R[Ω]の消費電力の測定値とする。
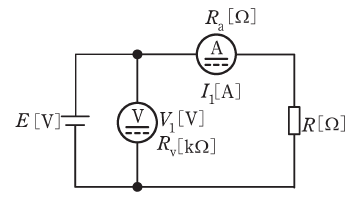
(a) 電流計の電力損失の値[W]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
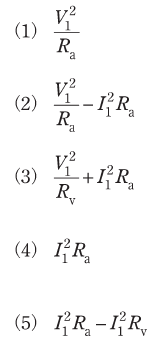
(b) 今、負荷抵抗R=320Ω、電流計の内部抵抗Ra=4Ωが分かっている。
この回路で得られた負荷抵抗R[Ω]の消費電力の測定値V1I1[W]に対して、R[Ω]の消費電力を真値とするとき、誤差率の値[%]として最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.3
- 0.8
- 0.9
- 1.0
- 1.2
解 説
(a)
電圧計にも電流計にも内部抵抗があるので、抵抗を強調して描くと、問題の回路図は下図のように描き換えることができます。
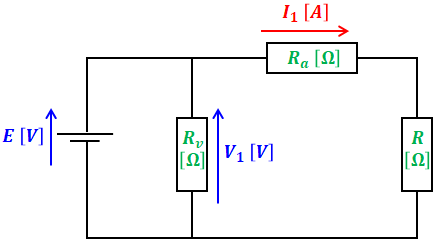
上図より、電流計を流れる電流はI1[A]、内部抵抗はRa[Ω]なので、電流計の電力損失の値Pa[W]は次のようになります。
![]()
よって、正解は(4)です。
(b)
(a)の解説で示した回路図に、(b)で与えられた条件を含めたものが以下の回路図です。この段階でわかっていない電流や電圧には適当な記号を付けています。
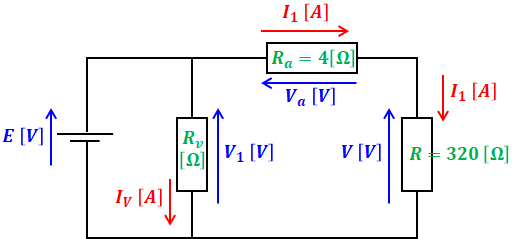
この問題で問われているのは、負荷抵抗R[Ω]の消費電力の測定値P測=V1I1[W]が、真の消費電力P真に対してどの程度ずれているかという、誤差率の値[%]です。
真値P真は上図より、次のようになります。
![]()
一方、測定値P測は(b)の問題文にもV1I1[W]と書かれている通り、電流計と電圧計のそれぞれの測定値の積です。
![]()
ここで、V1については上で示した回路図より、電源電圧Eと同じであることがわかります。
![]()
また、I1については上で示した回路図の電流計のところより、以下のように表すことができます。
![]()
上図の電流計の電圧Vaと負荷抵抗の電圧Vは勝手に付けた記号ですが、これらの和がV1であることは上図からわかっています。
また、電流計と負荷抵抗の抵抗値はそれぞれ4[Ω]と320[Ω]であるとわかっているので、その比から、VaはV1を使って次のように表されます。
![]()
(5)式を(4)式に代入すると、I1をV1を使った式にできます。
![]()
よって、(1)式と(2)式のそれぞれに(6)式を代入し、さらに(3)式を代入すると、P真とP測は次のようになります。
![]()
![]()
これで真値P真は(7)式で、測定値P測は(8)式で表せたので、誤差率εを計算していくことができます。
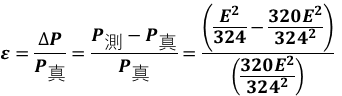
ここから、分母・分子のそれぞれをE2で割り、3242掛けると、以下のように誤差率εを求めることができます。
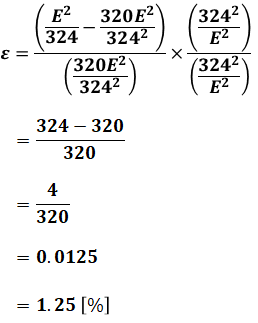
よって、最も近いものは(5)の1.2なので、正解は(5)です。

コメント