問 題
図は、ある周波数伝達関数W(jω)のボード線図の一部であり、折れ線近似でゲイン特性を示している。次の(a)及び(b)の問に答えよ。
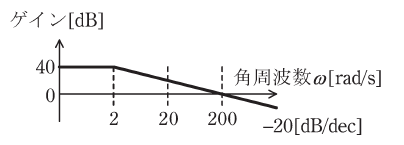
(a) 図のゲイン特性を示す周波数伝達関数として、最も適切なものを次の(1)~(5)のうちから一つ選べ。
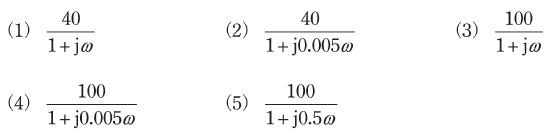
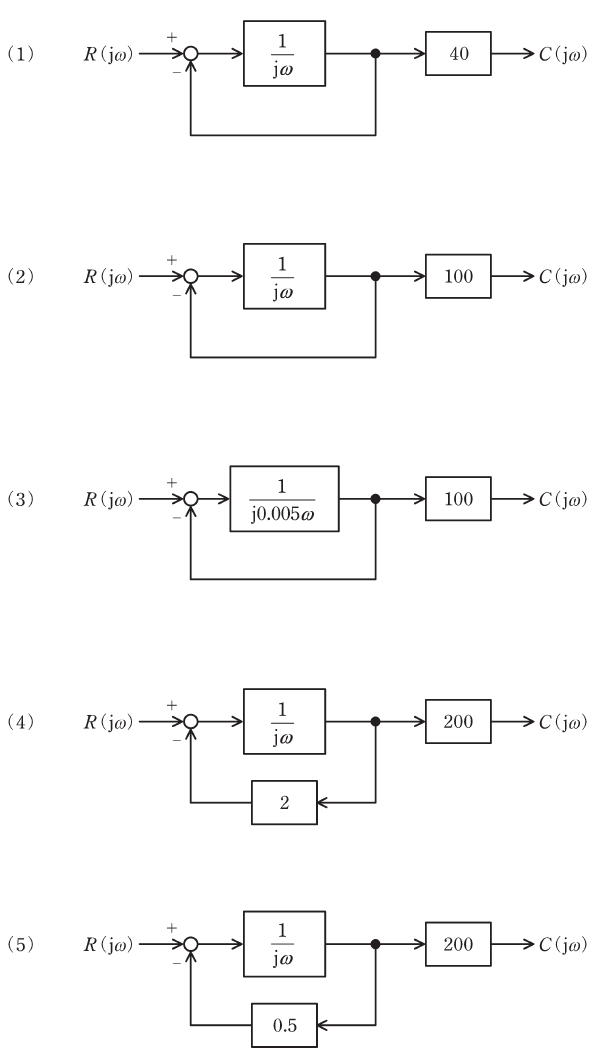
(b) 図のゲイン特性を示すブロック線図として、最も適切なものを次の(1)~(5)のうちから一つ選べ。ただし、入力をR(jω)、出力をC(jω)として、図のゲイン特性を示しているものとする。
解 説
(a)
最初に確認しておきたいのは、ゲイン特性は以下の式で表されるということです。この式は頻出とまではいえませんが、これを公式として覚えておかなくては正解するのが厳しい問題です。
![]()
- g:ゲイン[dB]
今回は、(1)式のW(jω)の部分が選択肢(1)~(5)のどれか、という問題です。選択肢の形はいずれも
![]()
となっているため、この(2)式を(1)式に代入すると次のように計算していくことができます。
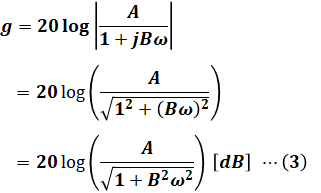
ここで問題文で与えられた図を見ると、たとえばω=0のときはg=40であり、ω=200のときはg=0であることがわかるので、上式にこれらの数値を代入してみます。今回はこの2つを代入してみますが、ω=2とg=40を使っても構いません。
ω=0、g=40を(3)式に代入すると、(4)式のようになります。
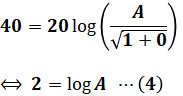
つまり、常用対数の底である10を2乗したのがAになるので、A=100だとわかります。この時点で選択肢は(3)~(5)に絞られます。
続いて、ω=200、g=0、A=100を(3)式に代入すると、(5)式のようになります。
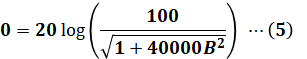
左辺が0なので、右辺を0にするためには真数(対数の底じゃないほう、つまりカッコの中身)を1にすればよく、以下のような計算ができます。
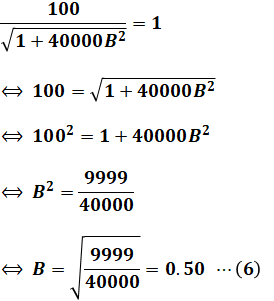
よって、B=0.5となります。
以上より、(2)式において、A=100かつB=0.5となっているのは選択肢(5)なので、正解は(5)です。
(b)
選択肢のブロック線図を見ると、どれもフィードバックの形をしています。フィードバックの伝達関数はブロック線図の中でも重要かつ頻出なので、ぜひ押さえておきたい内容です。
下図の左側のようなフィードバックモデルは右側のように簡略化できるので、入力をX(s)、出力をY(s)として式化すると次のようになります。これは最重要公式の一つとして覚えておいてください。なお、図中の「∓」が、式では「±」とひっくり返ることに注意が必要です。
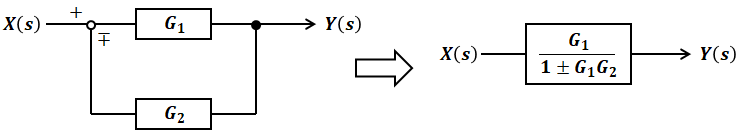
![]()
ただし、今回の問題では上記のような単純なフィードバックモデルではなく、各選択肢の右側にはさらに1つのブロックが付いています。つまり、次のような構成のブロック線図となっています。
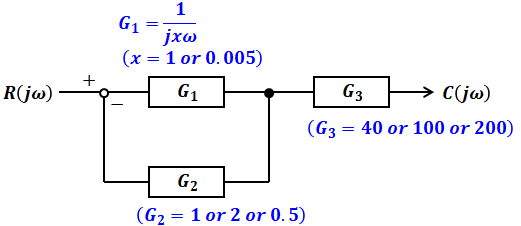
ちなみに、ブロック線図においては「1」の場合はブロックにならず、ただの線で表します。そのため、選択肢(1)~(3)の場合が「G2=1」であると考えてください。
上図において、フィードバック部分(G1とG2)は上記で示した公式の通りで、それとG3は直列に並んでいるため、これを式にする際は、単純な積で表すことができます。
よって、上図のブロック線図を式にすると、以下のようになります。
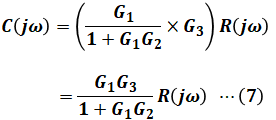
この(7)式の右辺の係数が設問(a)の答えと一致するようなG1、G2、G3の値がわかれば、それを表しているブロック線図が正解となります。
ここで、まずはG1を選択肢の形に合わせて、上のブロック線図で青字で示したように「G1=1/jxω」とします。G2やG3は単純な数値なのでそのまま使います。
すると、(7)式の係数部分は、次のように表すことができます。
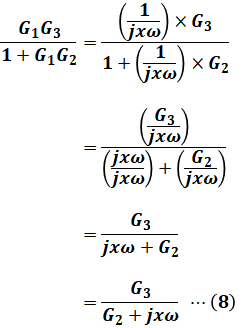
よって、(8)式と設問(a)の正解である(a)-(5)を見比べると、次のように考えることができます。
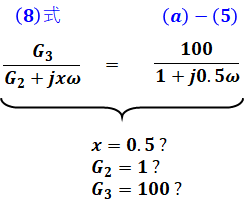
これで答えを出せれば良かったのですが、上記で示したブロック線図に青字で書いたように、選択肢からxの値は1か0.005の2択です。よって、(x, G2, G3)=(0.5, 1, 100)を満たすようなブロック線図は選択肢にありません。
しかし、(8)式を見ると、x,G2,G3を全て同じ数で掛けたり割ったりした場合、分母と分子が約分されるので全体の値は変わりません。よって、xを選択肢に合うような倍数で掛けて(または割って)みて、そのときのG2やG3も選択肢に合うようであれば、それが正解となります。
ここで、x,G2,G3を全て2倍にした(x, G2, G3)=(1, 2, 200)であれば、選択肢(4)の形と合うことがわかります。
以上から、正解は(4)です。

コメント