問 題
図のように、誘電体の種類、比誘電率、絶縁破壊電界、厚さがそれぞれ異なる三つの平行板コンデンサ①~③がある。極板の形状と大きさは同一で、コンデンサの端効果、初期電荷及び漏れ電流は無視できるものとする。
上側の極板に電圧V0[V]の直流電源を接続し、下側の極板を接地した。次の(a)及び(b)の問に答えよ。
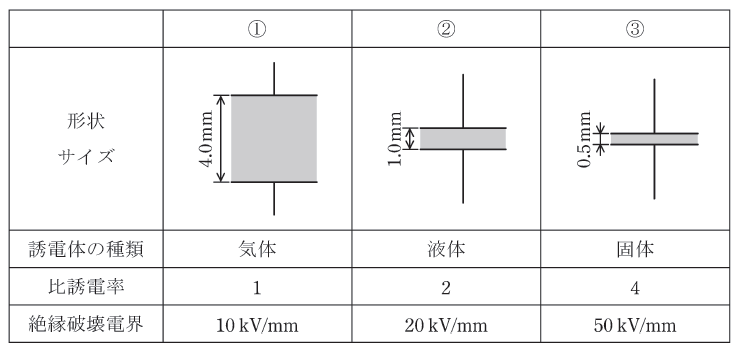
(a) 各平行板コンデンサへの印加電圧の大きさが同一のとき、極板間の電界の強さの大きい順として、正しいものを次の(1)~(5)のうちから一つ選べ。
- ① > ② > ③
- ① > ③ > ②
- ② > ① > ③
- ③ > ① > ②
- ③ > ② > ①
(b) 各平行板コンデンサへの印加電圧をそれぞれ徐々に上昇し、極板間の電界の強さが絶縁破壊電界に達したときの印加電圧(絶縁破壊電圧)の大きさの大きい順として、正しいものを次の(1)~(5)のうちから一つ選べ。
- ① > ② > ③
- ① > ③ > ②
- ② > ① > ③
- ③ > ① > ②
- ③ > ② > ①
解 説
(a)
問われているのは電界の強さEの大小関係なので、まずは電界Eの式を確認しておきます。これは重要公式として押さえておいてください。
![]()
- E:電界の強さ [V/m]
- V:電圧 [V]
- d:板間距離 [m]
(a)の問題文に「各平行板コンデンサへの印加電圧の大きさが同一」とあるので、①、②、③ともにVの値は同じです。つまり、dの値のみでEの値が決まります。上式を見るとわかるように、dが大きければEが小さくなり、dが小さければEが大きくなります。
よって、dは大きい順に、①の4.0mm、②の1.0mm、③の0.5mmとなるので、Eの大きさはその反対で「③ > ② > ①」の順番となります。
以上から、正解は(5)です。
(b)
問われているのは絶縁破壊電圧[V]です。一方で、問題の図では各コンデンサの絶縁破壊電界[kV/mm]と板間距離[mm]の値が与えられています。単位から考えるとわかりやすいですが、絶縁破壊電界[kV/mm]に板間距離[mm]を掛けたものが絶縁破壊電圧[V]となります。
よって、①、②、③のそれぞれの絶縁破壊電圧V絶は次のように計算することができます。
![]()
![]()
![]()
以上から、絶縁破壊電圧の大きさは「① > ③ > ②」の順番となるので、正解は(2)です。

コメント