問 題
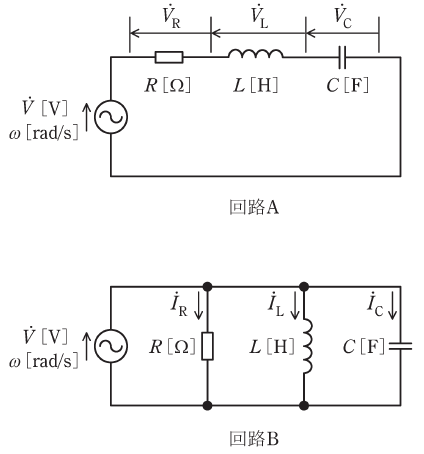
図のように、R[Ω]の抵抗、インダクタンスL[H]のコイル、静電容量C[F]のコンデンサと電圧![]() [V]、角周波数ω[rad/s]の交流電源からなる二つの回路AとBがある。
[V]、角周波数ω[rad/s]の交流電源からなる二つの回路AとBがある。
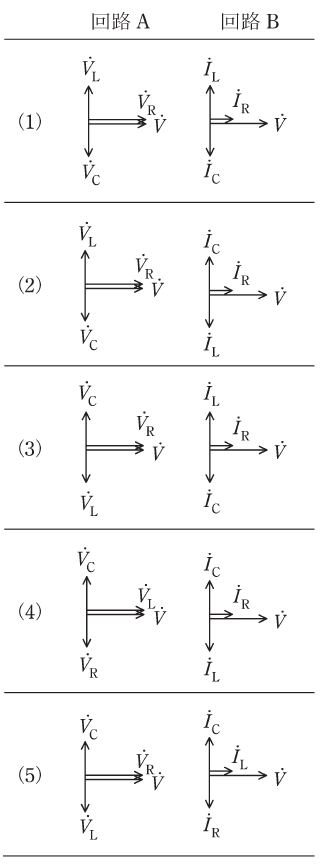
両回路においてそれぞれω2LC=1が成り立つとき、各回路における図中の電圧ベクトルと電流ベクトルの位相の関係として、正しいものの組合せを次の(1)~(5)のうちから一つ選べ。
ただし、ベクトル図における進み方向は反時計回りとする。
解 説
問題文の「ω2LC=1」を見たときに、これは共振回路だな。とパッと思いついてほしいです。「ωL=1/ωC」または「ω2LC=1」(どちらも同じことですが)が成り立つとき、コイルとコンデンサは共振を起こし、XLとXCが打ち消し合い、抵抗のみの回路を見なすことができます。
RLC直列共振回路(回路A)ではコイルやコンデンサが短絡したものとして扱うことができ、RLC並列共振回路(回路B)ではコイルやコンデンサが開放したものとして扱うことができます。要するに、どちらもコイルやコンデンサがなくなって、V=RIが成り立つ単純な回路と同等に扱えるということです。
この問題では、共振回路におけるコイルとコンデンサの打ち消し合い方が問われています。選択肢を見ると電圧や電流の向きが重要であることがわかりますが、LとCが向き合っていない選択肢(4)の回路Aや選択肢(5)の回路Bは明らかに誤りなので、まずこれらを除外できます。
ここで話が変わりますが、抵抗・コイル・コンデンサそれぞれに流れる電流の位相を確認しておきます。以下にまとめておきますので、これは最重要事項として覚えておいてください。
- 抵抗を流れる電流の位相は、電圧の位相と一致する
- コイルを流れる電流は、電圧に対してπ/2[rad](90°)だけ遅れる
- コンデンサを流れる電流は、電圧に対してπ/2[rad](90°)だけ進む
遅れとは、基準ベクトルに対して時計回りに回転する方向を指す言葉です。電流の変化が、電圧の変動に対して遅れることからこのように呼んでいます。反対に、進みは基準ベクトルに対して反時計回りに回転する方向です。
上記を基本事項として押さえておけば、回路Bの選択肢を見たとき、ILは時計回りに90°、ICは反時計回りに90°の位置になっている(2)が正しいと判断できます。
すでに答えは出ていますが、一応回路Aのほうも考えてみます。
回路Aでは電圧の位相が問われているため、今度は電流を基準に考えてください。先ほど示した「コイルを流れる電流は、電圧に対して遅れる」というのを言い換えると、「コイルの電圧は、電流に対して進む」となります。
一方、コンデンサのほうは「コンデンサの電圧は、電流に対して遅れる」といえます。これら先ほどの重要知識を言い換えているだけなので、改めて覚えておく必要はありません。
回路Aは直列回路なので、基準電流IはVRと同じ方向(横軸)になります。それを基準として、VLは進みなので反時計回りに90°、VCは遅れなので時計回りに90°の位置になることがわかります。
以上から、正解は(2)です。

コメント