電験三種 R2年 理論 問6 問題と解説

　問 題　　　　　

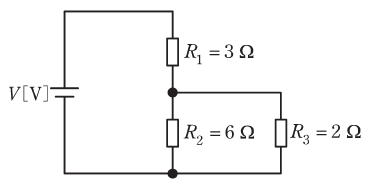
図のように、三つの抵抗R₁＝3Ω、R₂＝6Ω、R₃＝2Ωと電圧V[V]の直流電源からなる回路がある。

抵抗R₁、R₂、R₃の消費電力をそれぞれP₁[W]、P₂[W]、P₃[W]とするとき、その大きさの大きい順として、正しいものを次の(1)～(5)のうちから一つ選べ。

1. P₁ ＞ P₂ ＞ P₃
2. P₁ ＞ P₃ ＞ P₂
3. P₂ ＞ P₁ ＞ P₃
4. P₂ ＞ P₃ ＞ P₁
5. P₃ ＞ P₁ ＞ P₂

 

 

 

 

 

　解 説　　　　

電流I、電圧V、抵抗Rのうち2つがわかれば、以下の式を使って電力Pを求めることができます。

上式のうちどの組合せを使っても解くことができますが、今回はすでにRが与えられているので、電流と抵抗を使って問いてみます。ほかの方法を使って解いた方は、最後の答えさえ合っていれば、それも正しい解法だと思います。

まず、R₂とR₃は並列に並んでいるので、両者の端子電圧は同じです。よって、オームの法則V＝RIから、これらの抵抗比が6：2＝3：1なら、この抵抗を流れる電流の比は1：3になるはずです。

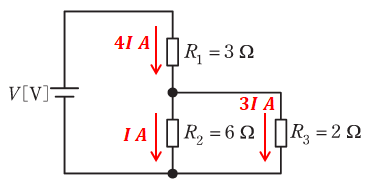
ここで、上図のようにR₂とR₃に流れる電流をそれぞれI、3Iとすると、R₁を流れる電流は4Iとなることがわかります。

よって、電力Pは、それぞれ次のように計算できます。

以上から、これらを大きい順に並べると、P₁、P₃、P₂の順になるので、正解は(2)です。