問 題
電気給湯器を用いて、貯湯タンクに入っている温度20℃、体積0.37m3の水を85℃に加熱したい。水の比熱容量は4.18×103J/(kg・K)、水の密度は1.00×103kg/m3であり、いずれも水の温度に関係なく一定とする。次の(a)及び(b)の問に答えよ。
(a) 貯湯タンク内の水の加熱に必要な熱エネルギーQの値[MJ]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 51
- 101
- 152
- 202
- 253
(b) 電気給湯器としてCOP(成績係数)が4.0のヒートポンプユニットを用いた。この加熱に要した時間は6時間であった。ヒートポンプユニットの消費電力Pの値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、ヒートポンプ式電気給湯器の貯湯タンク、ヒートポンプユニット、配管などの加熱に必要な熱エネルギーは無視し、それらからの熱損失もないものとする。また、ヒートポンプユニットの消費電力及びCOPは、いずれも加熱の開始から終了まで一定とする。
- 0.96
- 1.06
- 1.16
- 1.26
- 1.36
解 説
(a)
まず、水の密度が1.00×103kg/m3なので、水0.37m3の質量は次のように計算できます。
![]()
今回はこの水を65℃(=85-20)ほど上げるために必要な熱エネルギーQを計算すればよいので、その計算式は次のようになります。
計算方法は単位に注目すればわかりやすいと思いますが、比熱容量のところに出てくるK(ケルビン)は℃に置き換えられる点がポイントです。Kは絶対温度、℃は摂氏として使われますが、「温度差」として用いる限りは、両者を区別する必要はありません。
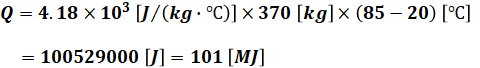
よって、正解は(2)となります。
(b)
まず、問題文よりヒートポンプユニットのCOP(成績係数)は4.0です。成績係数(COP)とは、ヒートポンプの効率を示す指標で、消費電力量Wに対する得られた熱エネルギーQで表されます。
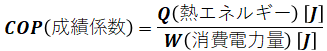
よって、これにCOP=4と(a)の結果を合わせると、次のようになります。
![]()
この問題で問われているのは消費電力量W[J]ではなく、消費電力P[W]です。単位の[W]は1秒あたりの電力量[J/s]のことなので、先ほど求めたW[J]を加熱に要した秒数で割ることで消費電力P[W]を求めます。
加熱に要した時間は問題文より6時間なので、以下のような計算により、消費電力Pを算出することができます。
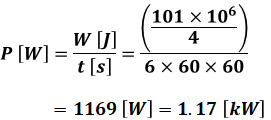
よって、選択肢の中で最も近い(3)が正解となります。

コメント