真空中に電子があり、もしそこに電界または磁界が存在するなら、この電子に力が働いて電子は運動します。より具体的には、電界中では電子は等加速度運動をし、磁界中では電子は円運動をします。
この項では電界中における電子の運動を解説し、次項にて磁界中における電子の運動を解説します。
下図のように、電界E[V/m]が存在している場に、電子を置いた場合を考えます。
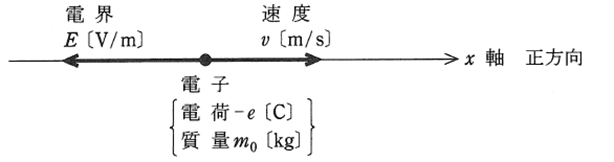
上図のように、電界E[V/m]はx軸上の負の方向に一定の大きさで存在するとして、電子の電荷は-e[C]、質量はm0[kg]とします(電子は負の電荷を持っているので、マイナスにしています)。
すると、静電気力F[N]は、電荷-e[C]と電界-E[V/m]との積で表すことができるので、電子の運動方程式は次のように表すことができます(電界にマイナスを付けているのは、この電子に加わる力(静電気力)の正方向をプラスとしているためです。上図を見てわかる通り、電子の運動方向(静電気力の向き)と電界の向きとは反対になります)。
![]()
- m0:電子の質量 [kg]
- a:電子の加速度 [m/s2]
- e:電子の電荷 [C]
- E:電界 [V/m]
これを加速度aについて解くと、
![]()
となります。上式の右辺のパラメータ(e、E、m0)は全て定数なので、加速度aはconst.(一定)であることがわかります。よって、この電子の運動は等加速度運動であるといえます。
また、等加速度運動であることがわかれば、速度v[m/s]は時間t[s]を使って次のように表すことができます(ちなみに、この手の問題では電子が最初の状態では止まっているため、初速度v0=0である場合が多いです)。
![]()
よって、電子の速度v[m/s]は時間t[s]の一次関数となります。
同様に、等加速度運動の距離x[m]と時間t[s]の関係は、以下の式の通りで、xはtの二次関数となります。
![]()
一方、電子の運動エネルギーの式も重要です。
上記では電界E[V/m]が存在している場で考えましたが、これは普通、平行平板電極間など有限の空間です。この電極の端から端までの電圧(陽極と陰極の電圧差)をV[V]とすると、電子がこの間を移動する際に、電界が電子に与える仕事は、eV[J]となります。
また、電界が電子にeV[J]の仕事を与えることによって、電子が1/2mv2[J]の運動エネルギーを得るので、これを結ぶと、
![]()
と表すことができます。
もし平行平板電極の負極を出発した電子が陽極にたどり着いたときの速度を知りたければ、上式をvについて解けばよいです。つまり、以下の式で表すことができます(上式を変形すれば導出できるので、無理に覚える必要はありません)。
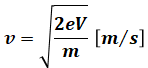

コメント