問 題
図のように、電圧線及び中性線の各部の抵抗が0.2Ωの単相3線式低圧配電線路において、末端のAC間に太陽光発電設備が接続されている。各部の電圧及び電流が図に示された値であるとき、次の(a)及び(b)の問に答えよ。
ただし、負荷は定電流特性で力率は1、太陽光発電設備の出力(交流)は電流I[A]、力率1で一定とする。また、線路のインピーダンスは抵抗とし、図示していないインピーダンスは無視するものとする。
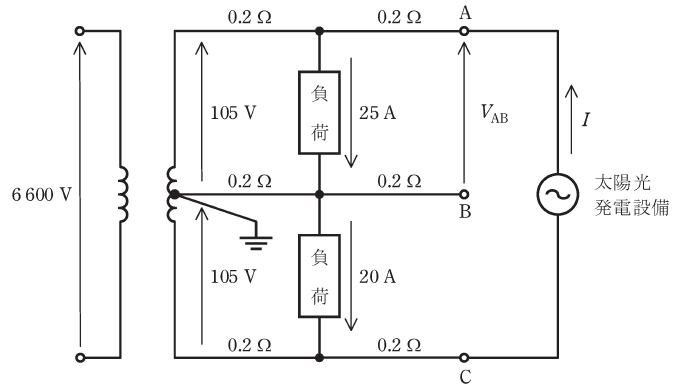
(a) 太陽光発電設備を接続する前のAB間の端子電圧VABの値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 96
- 99
- 100
- 101
- 104
(b) 太陽光発電設備を接続したところ、AB間の端子電圧VAB[V]が107Vとなった。このときの太陽光発電設備の出力電流(交流)Iの値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 5
- 15
- 20
- 25
- 30
解 説
(a)
(a)では太陽光発電設備が接続されていないので、問題文の図は下図のように描き換えることができます。
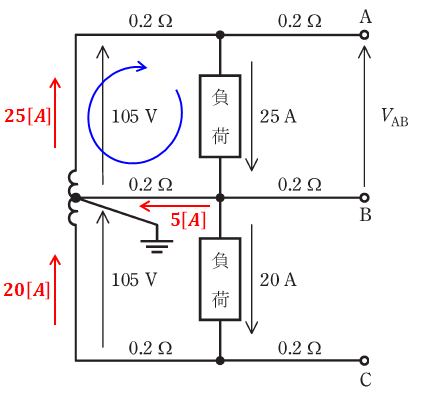
ここで、点A、点B、点Cのところは回路としてつながっていないので、一切電流は流れません。そのため、2つの負荷を流れる電流の差(25-20=5[A])が回路図の中央を左側へと流れることになります。
また、上図の青矢印で示した閉回路でキルヒホッフの法則を用いると、以下の等式が成り立ちます。
![]()
これをVABについて解くと、次のようになります。
![]()
よって、正解は(2)です。
(b)
(b)では太陽光発電設備が接続されているので、問題文の図をほとんどそのまま使います。ちなみに、今回も点Bのところは回路としてつながっていないため、ここには電流が流れません。
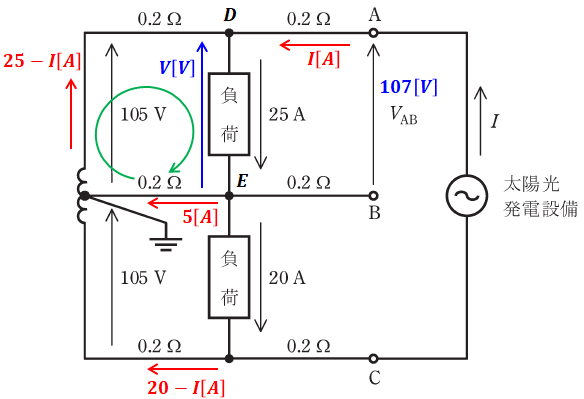
上図において、説明をしやすいように上側の負荷の両端を点D、点Eとします。ここで、DE間の電圧V[V]は、AB間の電圧と、AD間の電流と抵抗から、次のように表すことができます。
![]()
よって、上図の緑矢印で示した閉回路でキルヒホッフの法則を用いると、以下の等式が成り立ちます。
![]()
これをIについて解くと、次のようになります。
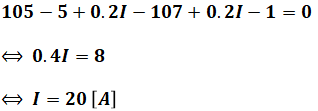
よって、正解は(3)です。

コメント