交流回路の力率改善

電源に負荷が接続されている交流回路において、その負荷の力率cosθは以下のように表すことができます。

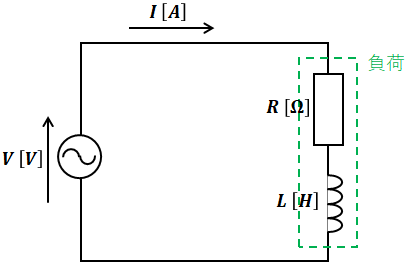
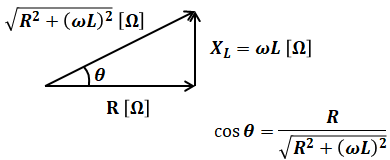
もし、この力率が低いと感じていて、もっと高くしたいと思うなら、負荷と並列にコンデンサを接続することが有効です。それは、コイルとコンデンサのリアクタンス[Ω]は位相が真逆(ベクトルの向きが反対)なので打ち消し合い、合成リアクタンスが小さくなった結果として、無効電力が減少するためです(有効電力は変わりません)。

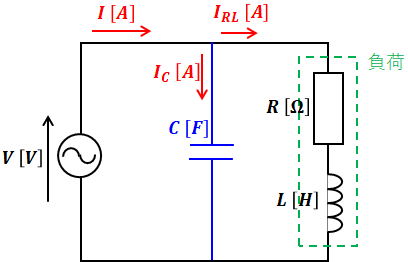
また、ここからはテクニックのような感じになってしまいますが、交流回路の力率改善の問題では上図の赤色矢印のように電流に注目すると良いです。

力率を1にするためには合成インピーダンスの虚数部を0にすればよい…と考えがちですが(それでも合っていますが)、「RとLの直列、かつCとの並列」という回路全体の合成インピーダンスを求めようとすると、計算がとても複雑になります。

そこで、上図のように、電源を流れる電流Iに対して、RとLを流れるほうをI_RL、Cを流れるほうをI_Cと分けて考えて、電源を流れる電流IをI=I_RL+I_Cと表し、そこの虚数部を0にする…というアプローチが、計算量も減るのでオススメです。

まずは簡単なほうで、コンデンサを流れる電流I_Cは、以下のように書くことができます。

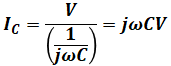
続いて、抵抗とコイルを流れる電流I_RLは次のようになります。

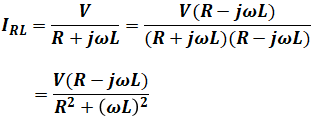
よって、電源を流れる電流Iはこれらを足せば良く、ついでに、実数部と虚数部を整理します。

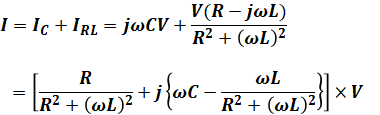
以上から、虚数部が0になるようにCの値を調整することで、電源を流れる電流の力率を1にすることが可能となります。つまり、力率が1になるようなCは次のように計算することができます。

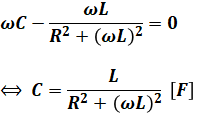
ちなみに、ここで紹介した式や図は、暗記しなくていいと思います。問題文によって素子の配置などが違うかもしれないので、以上の流れをしっかり押さえて、試験当日に自分で式を立てられるようにしておくことが重要です。