問 題
自家用水力発電所をもつ工場があり、電力系統と常時系統連系している。
ここでは、自家用水力発電所の発電電力は工場内において消費させ、同電力が工場の消費電力よりも大きくなり余剰が発生した場合、その余剰分は電力系統に逆潮流(送電)させる運用をしている。
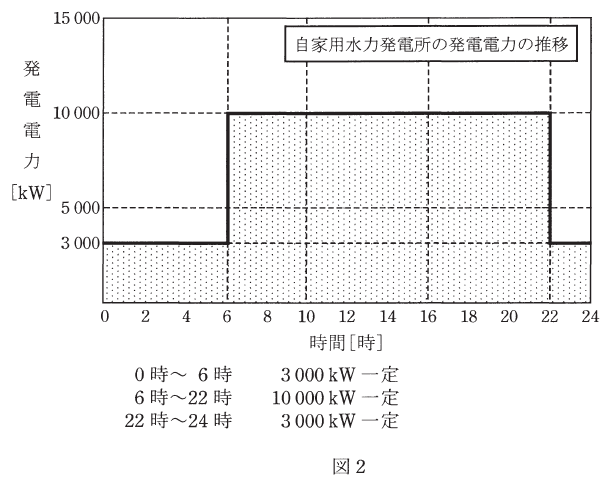
この工場のある日(0時~24時)の消費電力と自家用水力発電所の発電電力はそれぞれ図1及び図2のように推移した。次の(a)及び(b)の問に答えよ。なお、自家用水力発電所の所内電力は無視できるものとする。
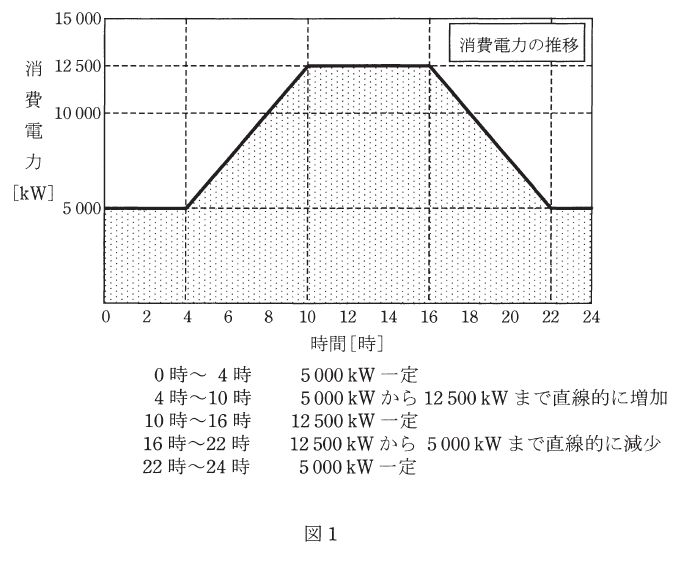
(a) この日の電力系統への送電電力量の値[MW・h]と電力系統からの受電電力量の値[MW・h]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
送電電力量[MW・h] 受電電力量[MW・h]
- 12.5 26.0
- 12.5 38.5
- 26.0 38.5
- 38.5 26.0
- 26.0 12.5
(b) この日、自家用水力発電所で発電した電力量のうち、工場内で消費された電力量の比率[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 18.3
- 32.5
- 81.7
- 87.6
- 93.2
解 説
(a)
図1(消費電力)と図2(発電電力)の図を重ねると、下図のようになります。
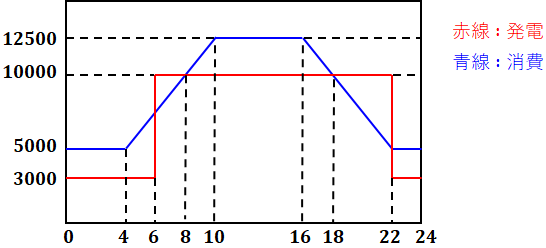
上図において、発電を示す赤線が消費を示す青線よりも上にある時間帯は送電、反対に青線が赤線よりも上にある時間帯は受電ということになります。よって、この日の送電量は下図の①と②の和になり、受電量は③~⑥の合計となります。
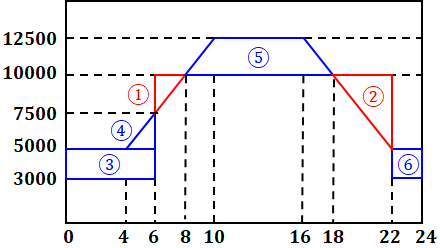
①と④について、どちらも三角形の底辺が2で合同な三角形なので、頂点同士がぶつかっている点の電力は7500となります。よって、①と④の面積はどちらも以下のように計算することができます。
![]()
![]()
続いて、②の三角形、③の長方形、⑤の台形、⑥の正方形についても同様に面積を求めます。
![]()
![]()
![]()
![]()
以上から、送電電力量と受電電力量はそれぞれ次のようになります。
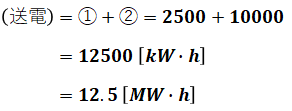
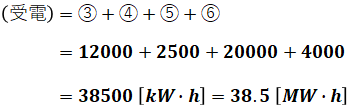
よって、正解は(2)です。
(b)
まずはこの日の発電電力量を計算します。
問題に記載された図2を見ると、3000kWが8時間分(0~6+22~24)と10000kWが16時間分なので、
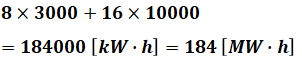
となります。
次に知りたいのは工場内で消費された分ですが、すでに(a)で送電電力量を求めているため、発電電力量から送電電力量を差し引けば、消費電力量を算出することができます。
![]()
以上から、発電電力量に対する消費電力量の比率は、次の通りとなります。
![]()

コメント