前項では、交流回路の電流や電圧の最も基本的な式を紹介しました。そこでは電流と電圧に位相差がないものとしましたが、それは電源のほかに抵抗しかない交流回路の場合です。
インダクタンスと静電容量の位相のページで解説したように、電源とコイル(インダクタンス)の回路では、位相はπ/2[rad](90°)だけ遅れます。また、電源とコンデンサ(静電容量)の回路では、位相はπ/2[rad](90°)だけ進みます。さらに、抵抗やコイルやコンデンサが組み合わさった回路では、位相がθ°の分だけ、進んだり遅れたりします。
この項では、前項で扱った電流と電圧の式を、抵抗、コイル、コンデンサ、負荷(2つ以上の素子の組み合わせ)の4パターンに分けて、それぞれ紹介していきます。
注意点として、ここで「遅れ」とか「進み」とかいう場合、電流が電圧に対して遅れている(または進んでいる)と解釈してください。つまり、どんなに位相が変わっても電圧の式は不動であり、電流の式が位相によって変わると考えます。
実際には、反対に電流を固定し電圧を動かしても構いませんが、どちらかに統一しないと混乱するので、このサイトでは、電圧を軸に電流の式を考える、というスタンスで解説します。
抵抗のみの回路
まずは素子が抵抗のみの交流回路における電流と電圧の正弦波の形と式を紹介します。これは前項で扱ったものと全く一緒です。
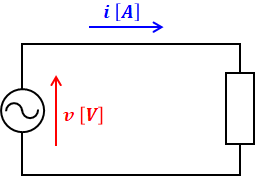
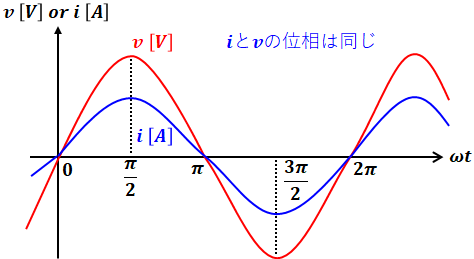
ちなみに、前項では上図の正弦波の横軸を時間tとしていましたが、今回はωtに変更しています。これはどちらでも差し支えないのですが、以下の式の都合上、ωtにしておけば、1周期がちょうど2π[rad](360°)で表されて視覚的にわかりやすいためです。
以上から、電流と電圧の式は次のようになります(VやIは実効値で、前項の通り、Vmax=√2V、Imax=√2Iです)。
![]() 、
、![]()
コイル(インダクタンス)のみの回路
次は、コイルのみの回路です。コイルのリアクタンスXL[Ω]は、抵抗R[Ω]に比べて、π/2[rad](90°)だけ遅れます。よって、電流の位相は、電圧に対してπ/2[rad](90°)だけ遅れることになります。
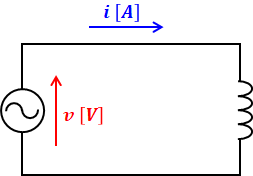
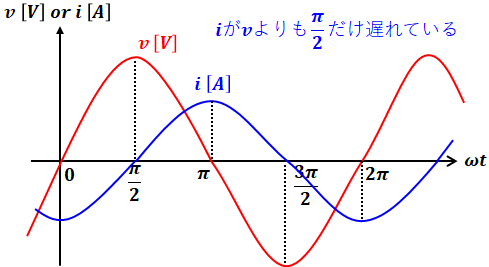
上図の青い正弦波が「遅れ」なのか「進み」なのかを判断するためには、赤い波と青い波の頂点の位置関係を見るとよいです。今回は、赤い波の頂点のちょっと右側に青い波の頂点があります。
横軸は時間tの関数なので(本当はωtですがω=2πfは定数だからtの関数となります)、より左側にある赤い波が先、青い波が後、となります。つまり、電圧が先で電流が後なので、電流は電圧よりも遅れているといえます。
また、電流と電圧の式は次のようになります。電圧の位相を基準としているため、電圧の式は抵抗のみのときと一緒です。
![]() 、
、![]()
コンデンサ(静電容量)のみの回路
続いてコンデンサのみの回路です。コンデンサのリアクタンスXC[Ω]は、抵抗R[Ω]に比べて、π/2[rad](90°)だけ進みます。よって、電流の位相は、電圧に対してπ/2[rad](90°)だけ進むことになります。
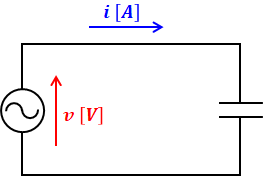
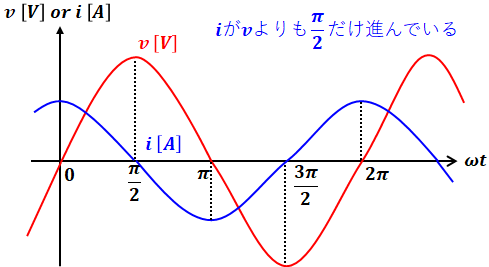
コンデンサはコイルと反対の関係になるので、電流や電圧の式は以下のとおりです。
負荷(素子が複数ある場合)の回路
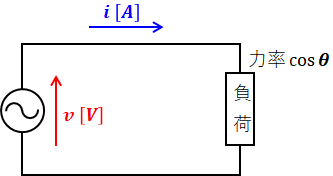
負荷の力率をcosθとした場合、位相差はθ[rad]となります。この場合の回路図、正弦波、電流と電圧の式は次のように表すことができます。
ここでは電流が電圧に対してθだけ遅れているという設定にしていますが、もちろん、進みとなることもあります(抵抗とコイルの回路なら遅れ、抵抗とコンデンサの回路なら進み、コイルとコンデンサが両方あればそれらのバランス次第)。

![]() 、
、![]()

コメント