直並列回路での共振

RLC直列回路とRLC並列回路の共振の条件式についてはそれぞれRLC直列共振回路のページとRLC並列共振回路のページで解説しました。どちらも同じ式で表すことができましたが、覚えておきたい大きな違いもあります。

それは、RLC直列共振回路では、合成インピーダンスZが最小になるということです。もう少し詳しくいえば、直列に並んだLC部分の合成インダクタンスX(X_LとX_Cの合成)が0となります。

一方、RLC並列共振回路では、合成インピーダンスZが最大(無限大)となります。こちらもLCだけに注目すると、並列に並んだLC部分の合成インダクタンスXが無限大(分母が0)です。

以上は単純なRLC直列回路やRLC並列回路での共振の話でした。このことを押さえておくことで得点につながる出題も多い一方で、たまに、直並列回路に関する出題もあるので、この項では上記2つを組み合わせた直並列回路における共振の計算方法について、例題を通して紹介します。

まず、問題設定を以下のように定めます。

例題

以下の図のような直並列回路があったとき、直列共振角周波数ω₁[rad/s]と並列共振角周波数ω₂[rad/s]の値をそれぞれ求めてください。

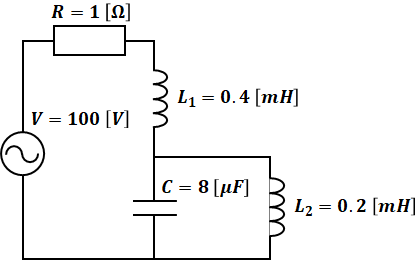
解説

重要なことは、(上記の繰り返しになりますが)直列共振の条件は合成インピーダンスZが最小になることで、並列共振の条件は合成インピーダンスZが最大になることです。よって、この問題のアプローチは、回路全体の合成インピーダンスZを求めるところから始めます。

回路全体のインピーダンスをZ[Ω]、コイルL₁、L₂、コンデンサCのリアクタンスをそれぞれ、X_L1[Ω]、X_L2[Ω]、X_C[Ω]とします。直並列回路のZを一発で計算式にするのは難しいので、まずは並列に並んだCとL₂の合成リアクタンスX_CL2を求めます。

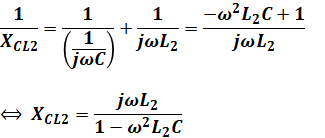
続いて、今求めたものと、R、L₁は直列に並んでいるので、それらの合成インピーダンスZは次のように計算できます。

ここで問題文に立ち返ると、求めたいのは直列共振角周波数ω₁(Zが最小)と並列共振角周波数ω₂(Zが最大)の2つです。

まずはZを最小にするほうから考えます。Zを最小にするには、上式の虚数部を0にすればよいです(ωを変えても実数部は不変であるため)。よって、次のような計算を行うことによって、ω₁を求めることができます(以下の計算過程は一例です。ほかの解き方や、先に数値を代入しても構いません)。

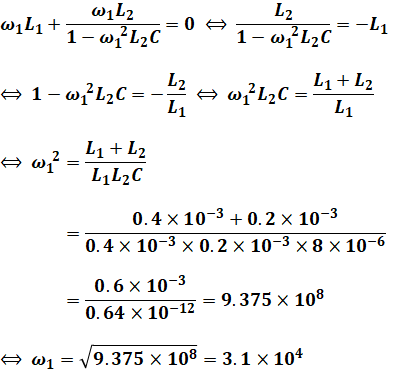
これがω₁の答えです。ちなみに、虚数部が0なので、このとき、Z=Rとなっています。

続いて、Zを最大にすることを考えます。今度は先ほどのZの式のうち、第3項の分母が0になるようにすれば、Zは極めて大きく(計算上は無限大に)なります。よって、次のような計算を行うことによって、ω₂を求めることができます。

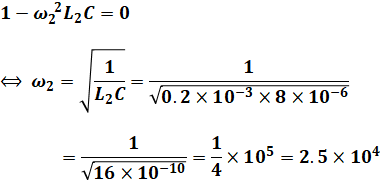
これがω₂の答えとなります。

ちなみに、今回は直列共振角周波数と並列共振角周波数の両方を計算したかったのでこのような解き方をしましたが、もし並列共振角周波数だけが問われていれば、RLC並列共振回路のページで解説したのと同様の考え方で解いても構いません。

つまり、並列に並んだコイルとコンデンサのリアクタンスが等しい(ωL=1/ωC)ときのωが並列共振角周波数なので、

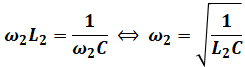
という計算式になりますが、結局は上記の解き方と同じ式につながります。

どう解き進めるかは好みの問題なので、ご自分に合うほうをお選びください。