前項までで扱ってきた直流回路では、電源のほかには抵抗しか使われない場合が多いです。一方、この項以降で扱う交流回路では、抵抗に似たものとしてインダクタンスと静電容量も使われます。
交流回路の素子には抵抗、コイル、コンデンサの3つがあり、コイルの性能を示すものがインダクタンス、コンデンサの性能を示すものが静電容量となります。
まずは、以下の図で直流回路(下図左側)と交流回路(下図右側)の違いを確認してください。
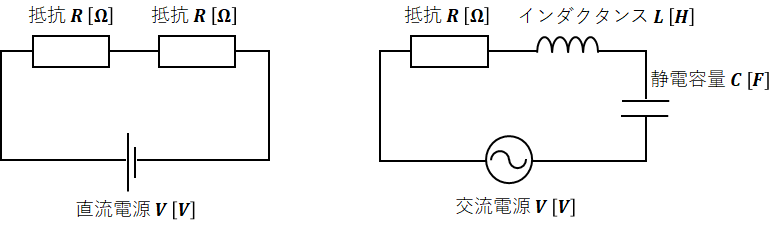
上図の左右を見比べると、まず電源の記号が違います。これで直流回路か交流回路かを判断することができます(電源の略号は参考書や問題集によってEになっていたりVになっていたりしますが、特に気にしなくて大丈夫です)。また、抵抗R[Ω]はともかく、インダクタンスL[H]や静電容量C[F]は、単位が[Ω]ではありません(これは重要!)。
このあたりを正確に理解していないと計算問題の最初でつまづくことになってしまうので、これらについて以下で整理します。
抵抗R[Ω]
抵抗Rについては、直流回路のときと同じように扱うことができます。たとえば複数の抵抗を合成しようとするとき、直列に並んでいれば和を計算すればよく、並列に並んでいれば、各抵抗の逆数の和が合成抵抗の逆数と一致します。
また、抵抗では電力P[W]が消費されますが、交流回路においては、これを特に有効電力P[W]と呼びます。ですが、やはり計算方法などは直列のときと一緒(P=IV=I2R=V2/R)なので、特に意識する必要はありません。
インダクタンスL[H]
インダクタンスLとはコイルの持つ能力のことです。回路図における記号は上図の通りくるくるしたコイル状のマークで、単位は[H]です(ヘンリーと読みます)。
より丁寧にいえば、コイルを流れる電流が変化すると誘導起電力が生じますが、その誘導起電力の大きさを決める係数となるのが、このインダクタンスです。…ですが、そんなことは覚えなくて大丈夫です。とにかく、インダクタンスLはコイルの性能だと思ってください。
大事なのはここからですが、インダクタンスを含む回路においても、計算問題ではやっぱりオームの法則を使います。しかし、単位が[H]のままではオームの法則が適用できないので、これを[Ω]に直す必要があります。そのための式が以下の式で、これは最重要公式としてぜひ覚えてください。
![]()
- XL:コイルのリアクタンス [Ω]
- L:インダクタンス [H]
- ω:角周波数 [rad/s]
- f:周波数 [Hz]
ωLを使うか2πfLを使うかは、問題文で与えられている情報から判断してください(ちなみに「ω=2πf」も重要公式です)。
インダクタンスやリアクタンス、次項以降で紹介するインピーダンスなど…名前が似ていて混乱するかもしれませんが、この区別がつかないと問題を解き進める上で大きな障害となってしまうので、ここはきちんと区別して覚えてください。コイルの能力がインダクタンスL[H]で、それを[Ω]に直したのがリアクタンスXL[Ω]です(単位に注目!)。
ちなみに、コイルに蓄えられる電力は、リアクタンスXL[Ω]を使えば抵抗の消費電力と同様に計算することができます。ただし、有効電力P[W]ではなく、こちらの場合は無効電力Q[var]といいます。単位の[var]はバールと読みます。
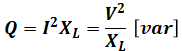
静電容量C[F]
静電容量CとインダクタンスLとは、似たような考え方で捉えることができます。上記(インダクタンスLの項)をしっかりと押さえておけば、こちらはさらっと読んでもらって構いません。
静電容量Cとはコンデンサの持つ能力のことです。回路図における記号は上図の通り同じ長さの2本の平行線で、単位は[F]です(ファラドと読みます)。
より丁寧にいえば、コンデンサにどのくらいの電荷を蓄えておけるかを表す容量のことを指す言葉ですが、コンデンサの能力値という認識で充分です。
こちらもオームの法則を使う際に、単位が[Ω]でないことが問題となります。よって、以下の式により、リアクタンスXC[Ω]に直す必要があります。これは最重要公式としてぜひ覚えてください。
![]()
- XC:コンデンサのリアクタンス [Ω]
- C:静電容量 [F]
- ω:角周波数 [rad/s]
- f:周波数 [Hz]
こちらの式は、コイルのときの逆数であることを押さえると、覚えやすいと思います。
コイルでもコンデンサでも、単位を[Ω]に直すと、同じリアクタンスと呼ばれることになります。よって、敢えて区別したい場合は、コイルのリアクタンス、コンデンサのリアクタンスのように明記します。ちなみに、略号のXLとXCから、コイルかコンデンサかを区別することもできます。
また、コンデンサに蓄えられる電力は、リアクタンスXC[Ω]を使ってコイルのときと同様に求められます。この場合も無効電力Q[var]となり式も一緒ですが、位相(ベクトル)が異なります(詳しくは次項で解説します)。
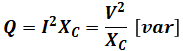

コメント