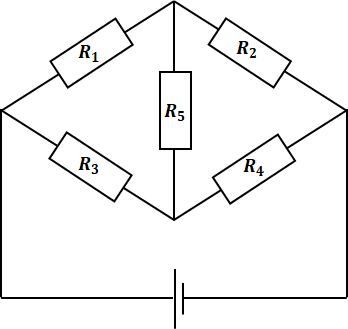
前項では、ブリッジ回路において平衡状態にあるときには以下の等式が成り立つことを紹介しました。
この項では、このホイートストンブリッジの原理が成り立つ理由について解説します。…が、電験三種の試験についてはこの原理の証明が必要になる機会はあまりないと思うので、参考程度に読んでください。特に理解しなくても、ブリッジ回路の形と抵抗(インピーダンス)の等式をしっかり押さえておけば、それで構わないと思います。
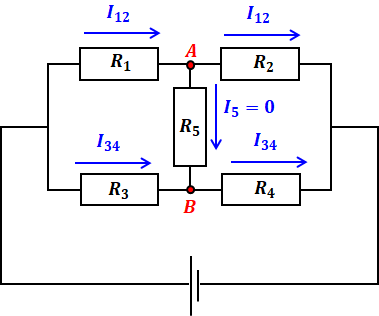
まず、ブリッジ回路が平衡状態にあるということは、R5に電流が流れないということなので、上記の回路のうち、R1とR2、R3とR4を流れる電流の大きさは、それぞれ等しくなります。
ここで、R5に電流が流れないなら、R5の両端の電圧は変わらないはずなので、点Aと点Bの電圧の差は0[V]です。よって、上図において、R1の両端の電圧とR3の両端の電圧は以下の(1)式のように等しくなり、R2とR4についても同様に、以下の(2)式の関係が成り立ちます。
(2)式を変形すると以下の(2)’式になり、これを(1)式に代入することで、最初に示した等式を導くことができます。
これが、ホイートストンブリッジの原理の導出過程になります。
以上では「平衡状態なのでR5に電流が流れない」→「R1×R4=R2×R3が成り立つ」の視点から証明しましたが、反対に「R1×R4=R2×R3が成り立つ」→「平衡状態となりR5に電流が流れない」というのも、キルヒホッフの法則などを使って計算を進めていけば証明することができます。
ここでは割愛しますが(試験ではその計算を要求されないと思うので)、興味のある方はぜひ試してみてください。

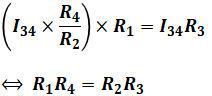
コメント