重ね合わせの原理(基礎)

電気回路の電流や抵抗を計算する際に、覚えておきたいルールがいくつかあります。たとえば、キルヒホッフの法則、重ね合わせの原理、鳳・テブナンの定理などです。前項では最重要事項であるキルヒホッフの法則を扱ったので、この項と次項では重ね合わせの原理を解説します。

重ね合わせの原理は、多電源回路(電源が2つ以上ある場合)の計算問題で便利なルールです。以下にこの原理の使い方を説明しますが、電源が複数あるときに使えるという点もぜひ押さえておいてください。

重ね合わせの原理とは、電源が複数ある電気回路において、それぞれの電源が1つしかないものと仮定して計算した場合に、それらの和がもとの電気回路の値と一致する、というものです。文字にするとわかりにくいので、以下に簡単な電気回路を例に挙げて説明します。

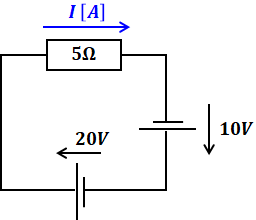
上図において、抵抗を流れる電流Iはいくつでしょう、と問われたとします。これは単純な回路なので、電源の和が30Vだから30÷5=6[A]とすぐ計算することができますが、これを重ね合わせの原理を用いて計算すると次のようになります。

まず、一方の電源だけ残して、他方の電源を消します(短絡させます)。

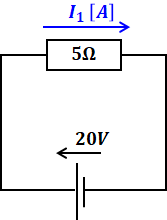
すると、I₁=4[A]と計算することができます。

続いて、先ほどと反対の電源を残し、他方の電源を消します(短絡させます)。

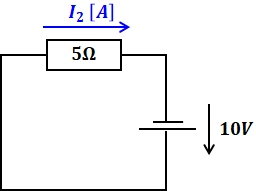
すると、I₂=2[A]と計算することができます。

よって、もともとの電気回路においての電流Iは、I=I₁+I₂=4+2=6[A]となります。

これが、重ね合わせの原理の計算方法です。ただし、上記のような簡単な電気回路ではこの原理を使うメリットがわかりにくいと思います。次の項で少し複雑な(実践的な)電気回路を用いた例題を示しますので、ぜひ練習してみてください。