問 題
下記の諸元の揚水発電所を、運転中の総落差が変わらず、発電出力、揚水入力ともに一定で運転するものと仮定する。
この揚水発電所における発電出力の値[kW]、揚水入力の値[kW]、揚水所要時間の値[h]及び揚水総合効率の値[%]として、最も近い値の組合せを次の(1)~(5)のうちから一つ選べ。
揚水発電所の諸元
- 総落差:H0=400m
- 発電損失水頭:hG=H0の3%
- 揚水損失水頭:hP=H0の3%
- 発電使用水量:QG=60m3/s
- 揚水量:QP=50m3/s
- 発電運転時の効率:発電機効率ηG×水車効率ηT=87%
- ポンプ運転時の効率:電動機効率ηM×ポンプ効率ηP=85%
- 発電運転時間:TG=8h
発電出力[kW] 揚水入力[kW] 揚水所要時間[h] 揚水総合効率[%]
- 204600 230600 9.6 74.0
- 204600 230600 10.0 71.0
- 198500 237500 9.6 71.0
- 198500 237500 10.0 69.6
- 198500 237500 9.6 69.6
解 説
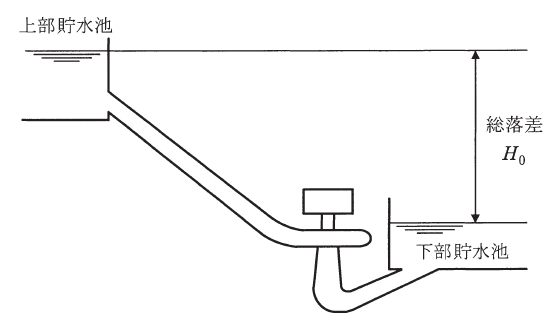
水力発電は水の位置エネルギーを電気エネルギーに変えるものなので、発電機出力PGは次の式で表すことができます。
![]()
- PG:発電出力 [kW]
- QG:発電使用水量 [m3]
- H:有効落差 [m]
- ηT:水車効率 [%]
- ηG:発電機効率 [%]
ここで、実際の落差(総落差)は400mですが、損失分(発電損失水頭)が3%分あるので、有効落差は総落差の97%分となります。よって、上式にそれぞれの値を代入すると、以下のようになります。
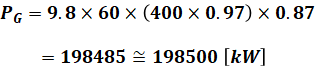
一方、揚水入力PPについては、発電のときのちょうど反対のことをするだけなので、その式もPGを求める式とほとんど一緒です。
![]()
- PP:揚水入力 [kW]
- QP:揚水量 [m3]
- H:有効落差 [m]
- ηM:電動機効率 [%]
- ηP:ポンプ効率 [%]
ただし、揚水入力の式と発電出力の式で大きく違う点が2つあります。
発電出力を求める際には、理論的なエネルギーから損失を除いたものが出力になりましたが、揚水入力の計算では、求めるエネルギーを得るために理論的な揚水入力に加えて損失となる分のエネルギーも合わせて入力しなくてはならないので、効率は分子ではなく分母にきます。
また、同様の理由で、発電出力の式では総落差に対して損失分を引いたものが有効落差となりましたが、揚水入力の式では、損失を加味すると総落差以上に持ち上げなければならないので、有効落差は総落差に損失分を足したものとなります。
よって、上式にそれぞれの値を代入すると、以下のようになります。
また、この問題では揚水した水を再び落とすことで発電しているので、揚水と発電の際に扱う水の量は同じです。
※ 問題を解く前に、ちょっと蛇足というか、補足説明をします(この問題とは関係ありません)。
揚水してまた落とす、と書いてしまっては全く無駄なことをしているように思えるかもしれませんが、そうではありません。
揚水発電は、供給する電力が余っている時間帯(皆が電気を使わない夜など)に揚水を行って、電力需要が大きくなった頃合いを見計らって落水して発電をしています。
よって、揚水で損失が生まれて、発電でまた損失が生まれるのは確かに無駄になってしまうのですが、揚水発電の仕組み自体は意味のある行為です。
では、問題に戻ります。
1秒間あたりの発電使用水量QGと1秒間あたりの揚水量QPは60:50なので、使う水の量が同じ場合、所要時間は反対の50:60=5:6になります。そして、発電運転時間TGは8hとわかっているので、揚水所要時間TPは、
![]()
と計算することができます。
最後は揚水総合効率を求める問題ですが、これは要するに入力エネルギーに対する出力エネルギーが何%かということが問われています。すでに入力と出力それぞれのkW数と時間がわかっているので、エネルギーはその積となります。
よって、揚水総合効率は次のように計算することができます(本来なら「1h」を「3600s」に直したりしたほうがいいかもしれませんが、比の問題なのでそのまま計算して大丈夫です)。
![]()

コメント