キルヒホッフの法則

電気回路の電流や抵抗を計算する際に、覚えておきたいルールがいくつかあります。たとえば、キルヒホッフの法則、重ね合わせの原理、鳳・テブナンの定理などです。この項では、その中でも最も重要であるキルヒホッフの法則について解説をします。ちなみに、キルヒホッフの法則には第一法則と第二法則の2つがあります(どちらも大事です)。

キルヒホッフの第一法則(電流則)

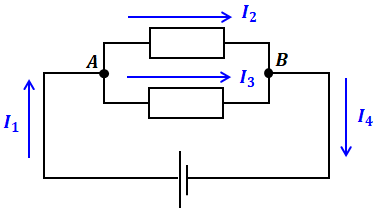
キルヒホッフの第一法則は、電流則ともいわれます。ルールとしては単純で、以下の図と式のようなものです。

つまり、電流が分岐する点Aに注目したとき、そこに流れ込む電流(I₁)とそこから流れ出る電流の和(I₂+I₃)が等しくなります。同様に、電流が合流する点Bでも、流れ込む電流の和(I₂+I₃)とそこから流れ出る電流(I₄)が等しくなります。

キルヒホッフの第二法則(電圧則)

キルヒホッフの第一法則が電流則と呼ばれるのに対し、第二法則は電圧則ともいわれます。電気回路のある点から閉回路をぐるっと1周すると、その間に電圧は上がったり下がったりしますが、もとの点に戻るときには電圧も元通り(電圧変化の総和は0)になる、というのが第二法則です。

たとえば、以下の電気回路において、点Aから左半分の閉回路を時計回りに回ると(赤矢印)、以下のような計算により電圧変化の総和は0になります。

また、点Aから右半分の閉回路を反時計回りに回っても(青矢印)、同様に電圧変化の総和は0になります。

もちろん、点Aから図の回路の外側を大回りしても、同様の結果が得られます(以下の式は時計回りで計算)。この場合、電源や電流の向きに気をつけて正負を正しく計算してください。

これら2つのキルヒホッフの法則を使えば、電気回路の中で未知の電流や電圧、抵抗などがあっても、等式を立てて計算することで、未知数を求めることができるようになります。