問 題
図のように、十分大きい平らな金属板で覆われた床と平板電極とで作られる空気コンデンサが二つ並列接続されている。二つの電極は床と平行であり、それらの面積は左側がA1=10-3m2、右側がA2=10-2m2である。
床と各電極の間隔は左側がd=10-3mで固定、右側がx[m]で可変、直流電源電圧はV0=1000Vである。次の(a)及び(b)の問に答えよ。
ただし、空気の誘電率をε=8.85×10-12F/mとし、静電容量を考える際にコンデンサの端効果は無視できるものとする。
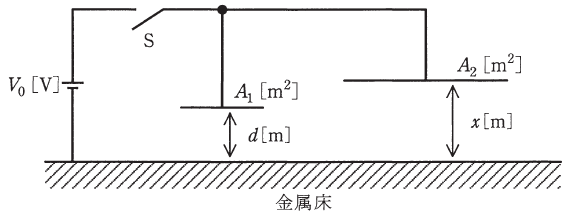
(a) まず、右側のx[m]をd[m]と設定し、スイッチSを一旦閉じてから開いた。このとき、二枚の電極に蓄えられる合計電荷Qの値[C]として最も近いものを次の(1)~(5)のうちから一つ選べ。
- 8.0×10-9
- 1.6×10-8
- 9.7×10-8
- 1.9×10-7
- 1.6×10-6
(b) 上記(a)の操作の後、徐々にxを増していったところ、x=3.0×10-3mのときに左側の電極と床との間に火花放電が生じた。左側のコンデンサの空隙の絶縁破壊電圧Vの値[V]として最も近いものを次の(1)~(5)のうちから一つ選べ。
- 3.3×102
- 2.5×103
- 3.0×103
- 5.1×103
- 3.0×104
解 説
(a)
電荷Qが問われていますが、これはコンデンサに関する2つの最重要公式を組み合わせることで計算できます。
![]()
- Q:電荷[C]
- C:静電容量[F]
- V:電圧[V]
![]()
- ε:誘電率[F/m]
- A:板の面積[m2]
- d:板間距離[m]
まずは(2)式に問題文で与えられた数値を代入すると以下のようになります。ここでは、問題の図の左側のコンデンサの静電容量をC1、右側のほうをC2としています。
![]()
続いて、これを(1)式に代入すると、2つのコンデンサに蓄えられる電荷の合計値Qは次のようになります。
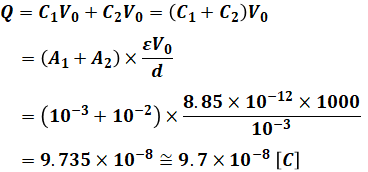
以上から、正解は(3)です。
(b)
設問(a)の操作直後の回路図は以下の左側、火花放電が生じたときの回路図は以下の右側のように描くことができます。スイッチはずっと開いているので電源については考える必要がないため、以下の回路図にも記載していません。
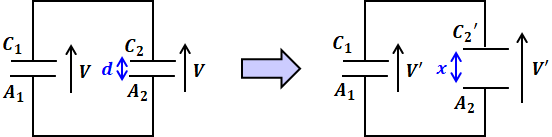
上図の左側から右側に移る際、この回路は閉じたままなので、コンデンサの電極の間隔を変えて静電容量C2‘の値が変動したとしても、回路内に存在する電荷Qは変わりません。
よって、上図右側のQも設問(a)で求めた上図左側のQと等しいことから、以下の等式を解くことによってV’を求めることができます。
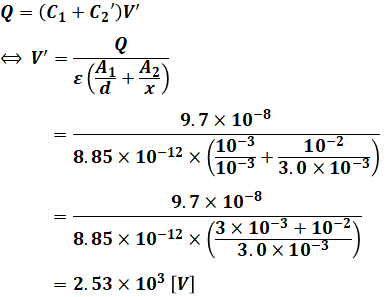
以上から、正解は(2)です。

コメント