自己インダクタンスについてはこちらのページで、相互インダクタンスについてはこちらのページで解説しましたが、この項ではそれらのまとめと、両者を組み合わせた式について紹介します。
自己インダクタンス
環状鉄心に2つの導線を巻いて2つのコイルを作ったとき、それぞれの自己インダクタンスL1、L2は次式で表されます(各パラメータの右下の数字は、コイル1またはコイル2に対応すると考えてください)。
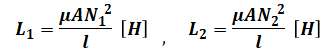
- L:自己インダクタンス [H]
- μ:環状鉄心の透磁率 [H/m]
- A:環状鉄心の断面積 [m2]
- N:巻数
- l:磁路の長さ [m]
相互インダクタンス
一方、相互インダクタンスMは次のように書くことができます。
![]()
- M:相互インダクタンス [H]
これと自己インダクタンスLの式を組み合わせると、Mは以下のようにL1とL2を使って表すことができます(式の導出についてはこの項の最後に紹介します)。
![]()
ただし、上式が成り立つのは理想的な条件での話であり、実際には漏れ磁束での損失分があるため、係数kを掛ける必要があります。このkを結合定数といい、0~1の範囲の値をとります。理想的な条件ではk=1です。
よって、相互インダクタンスと自己インダクタンスをつなぐ式は以下のようになります。
![]()
- M:相互インダクタンス [H]
- k:結合係数(0~1)
- L1、L2:自己インダクタンス [H]
合成インダクタンス
環状鉄心にコイルが2つ巻いてある場合、自己インダクタンスだけでなく相互インダクタンスも生じます。これらはどちらかだけ発生するものではなく両方が同時に存在するので、それらを合わせて考えることもあります。
自己インダクタンスと相互インダクタンスを合わせたものを合成インダクタンスといいますが、2つのコイルで発生する磁束の向きが同じ方向(強め合う方向)となるような接続の仕方を、和動接続といいます。反対に、2つのコイルでの磁束が打ち消し合って弱め合うような接続の仕方を、差動接続といいます。
和動接続と差動接続のそれぞれについて、合成インダクタンス(Lwa、Lsa)は次の式で表すことができます。
![]()
![]()
- Lwa:和動接続での合成インダクタンス [H]
- Lsa:差動接続での合成インダクタンス [H]
- L1:コイル1の自己インダクタンス [H]
- L2:コイル2の自己インダクタンス [H]
- M:相互インダクタンス [H]
(参考) M=√L1L2の導出
参考までに紹介しますが、相互インダクタンスMを自己インダクタンスL1、L2を用いて表す式の導出は以下の通りです。上記の式は公式として覚えてしまえばよいと思うので、以下の計算過程は参考程度に確認してみてください。
まず、L1、L2の式をそれぞれN1、N2について解きます。

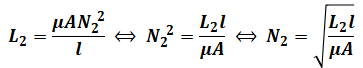
これをMの式に代入して整理していけば、MをL1、L2で表す式が導けます。
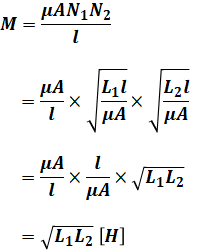

コメント