問 題
次の真理値表の出力を表す論理式として、正しい式を次の(1)~(5)のうちから一つ選べ。

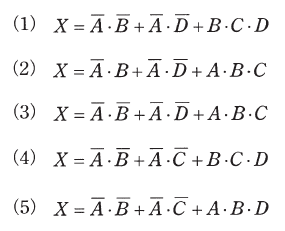
解 説
このような問題では、全パターンの論理式を式化して考えると計算が複雑になるので、以下のようなカルノー図を使って考えるのが有効です。
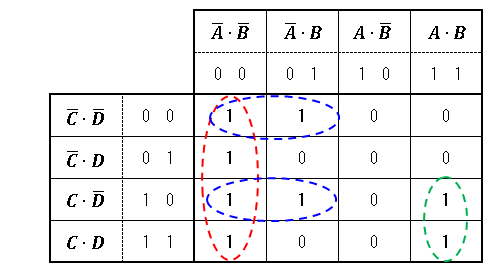
ここでは横にAとBを、縦にCとDを並べていますが、特にどのような組み合わせでも構いません。しかし、5つの選択肢のどれにも最初の項がAとBの積になっているので、AとBを合わせたほうが考えやすいです。
カルノー図の描き方は、最初、A・Bの4つの組み合わせ(00、01、10、11)を記入し、C・Dも同様に書きます。その後、A・BとC・Dの組み合わせによって4×4=16通りのマスがありますが、問題文にある論理式を見ながら、この16マスに出力Xを0か1で入れていきます。
たとえば、問題文の論理式の上から4つ分はどれもAとBが0で、Xは全て1です。つまり、AもBも0なら、CやDに関係なくX=1になるので、上図の左端の列はいずれも1と記入できます。同様に考えていくと、16マス全てに0か1を入力していくことができます。
実際には、論理式からX=1になるものだけを調べればよいです。あとは全て0になります(今回はX=0とX=1が8つずつで等しいですが、もし偏りがあれば、少ないほうだけを数えると早いです)。
このようにしてカルノー図が描けたら、これを式化していけばよいのですが、その際、選択肢を使うと便利です。この問題の選択肢では、第1項がいずれもAとBの組み合わせになっています。しかも、(A,B)=(0,0)or(0,1)の2択なので、この2つについてカルノー図の該当箇所を確認します。
すると、(A,B)=(0,0)のときは赤枠で示している通り、全てX=1となっているので、これが正しいといえます。一方、(A,B)=(0,1)だとXが0だったり1だったりするので不適です。
続いて選択肢の第2項を見てみると、ここは(A,C)=(0,0)or(A,D)=(0,0)の2択となります。先ほどと同様に見ていくと、青枠で示している(A,D)=(0,0)のほうが正しいことがわかります。
ここまでで選択肢は(1)か(3)に絞られているので、第3項は(1)と(3)の分だけ調べれば充分です。つまり、(A,B,C)=(1,1,1)と(B,C,D)=(1,1,1)についてカルノー図の該当箇所を見ることになります。すると、(A,B,C)=(1,1,1)のときに緑枠で示した通りX=1となるので、正解は(3)と判断することができます。

コメント