前項で紹介した自己インダクタンスと併せて押さえておきたいのが、この項で解説する相互インダクタンスです。下図のように、環状鉄心の2箇所に電線が巻いてあり、独立した2つのコイルがある状況を考えてください。
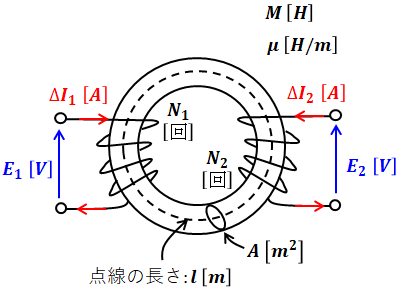
このとき、それぞれのコイルには自己インダクタンスが生じます。自己インダクタンスは、コイルを流れる電流が変化した際、磁束が変化して自己誘導起電力が生じるために発生するものでした。
今回のようにコイルが2つある場合、一方のコイルで磁束が変化すれば、磁界はつながっているので他方のコイルにも影響が出ます。そうすると、影響を受けたコイルのほうでも起電力が生じます。この起電力のことを相互誘導起電力といいます。
相互誘導起電力の大きさは次式によって表されます(各パラメータの右下の数字は、コイル1またはコイル2に対応すると考えてください)。
- E:誘導起電力 [V]
- M:相互インダクタンス [H]
- ΔI:電流の変化量 [A]
- Δt:時間 [s]
上式は何か見覚えがあるかもしれませんが、これは自己誘導起電力の式とかなり似ています。自己誘導起電力と相互誘導起電力は併せて覚えておけば記憶しやすいと思います。
また、上式にも出てきていますが、相互誘導起電力によって生じるのが相互インダクタンスです。相互インダクタンスM[H]の大きさは、以下の式で表すことができます。M12はコイル1に流れる電流の影響でコイル2に生じるインダクタンスを表し、M21はその逆だと考えてください。これも自己インダクタンスの式と似ているので、一緒に押さえておきたい公式です。
- M:相互インダクタンス [H]
- N:巻数
- Φ:磁束 [Wb]
- I:電流 [A]
- μ:環状鉄心の透磁率 [H/m]
- A:環状鉄心の断面積 [m2]
- l(エル):磁路の長さ [m]
上式を見てもわかるように、M12でもM21でも、μ、A、N1、N2、lを使った式では、全く同じ形で表すことができます。

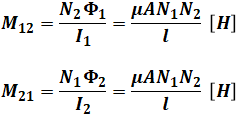
コメント