電験三種 H27年 電力 問17 問題と解説

　問 題　　　　　

図に示すように、線路インピーダンスが異なるA、B回線で構成される154kV系統があったとする。A回線側にリアクタンス5%の直列コンデンサが設置されているとき、次の(a)及び(b)の問に答えよ。なお、系統の基準容量は、10MV・Aとする。

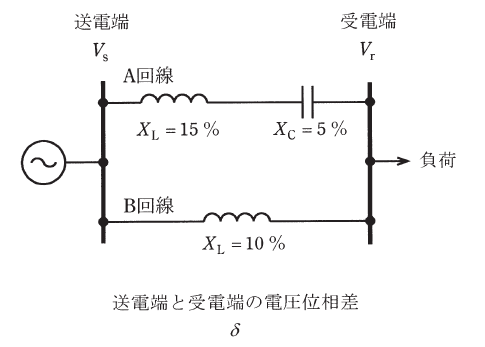
(a)　図に示す系統の合成線路インピーダンスの値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 3.3
2. 5.0
3. 6.0
4. 20.0
5. 30.0

(b)　送電端と受電端の電圧位相差δが30度であるとき、この系統での送電電力Pの値[MW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、送電端電圧V_s、受電端電圧V_rは、それぞれ154kVとする。

1. 17
2. 25
3. 83
4. 100
5. 152

 

 

 

 

 

　解 説　　　　

(a)

%インピーダンス(%Z)の基準容量が一致している場合、直列に並ぶ%Zはそのまま足し算ができます。また、並列に並ぶ場合は、各%Zを逆数にしてから足し算をして、その逆数を戻せば合成することができます。要するに、抵抗の合成と計算方法は一緒です。

今回は問題文に「系統の基準容量は、10MV・Aとする」とあるので、3つの%Zはどれも基準容量が一致しています。よって、まずは直列に並んだA回線の2つを合成すると、

となります。ここで、コイルとコンデンサとでは、符号が反対になる点に注意してください。その後、A回線とB回線での並列の合成を行うと、

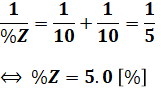
と計算することができます。

(b)

送電電力Pを求める問題ですが、送電電力を求める以下の式は公式として覚えておいたほうがよいです。

• P：三相3線式送電線の送電電力(有効電力) [W]
• V_s：送電端の線間電圧 [V] (supplyの”s”)
• V_r：受電端の線間電圧 [V] (receiveの”r”)
• X：線路リアクタンス [Ω]
• δ：V_s－V_r間の相差角

今回は、問題文によりV_sとV_rがともに154kVであり、電圧位相差δも30°と与えられているので、未知なのは線路リアクタンスXだけです。

(a)で%Zを求めているので、%ZとインピーダンスZをつなぐ以下の式を使って、Zを計算します(ちなみに、インピーダンスZとは、抵抗RとリアクタンスXの合力のことです。この問題では抵抗は登場しないので、Z=Xとなることを理解しておいてください)。

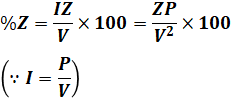
• P：基準容量[V・A]
• V：線間電圧[V]
• I：電流[A]

上式に、問題で与えられた数値を代入していくと、

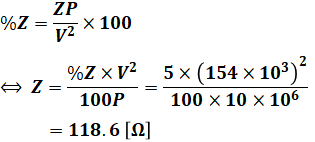
となり、これを先ほどの送電電力の式に代入すると(上記の通りZ=Xです)、

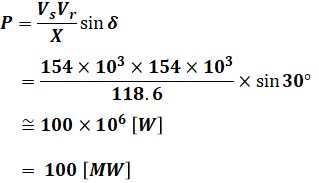
と計算することができます。