問 題
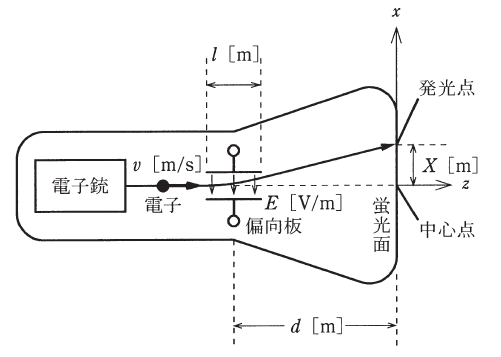
ブラウン管は電子銃、偏向板、蛍光面などから構成される真空管であり、オシロスコープの表示装置として用いられる。図のように、電荷-e[C]をもつ電子が電子銃から一定の速度v[m/s]でz軸に沿って発射される。
電子は偏向板の中を通過する間、x軸に平行な平等電界E[V/m]から静電力-eE[N]を受けx方向の速度成分u[m/s]を与えられ進路を曲げられる。偏向板を通過後の電子はz軸と![]() なる角度θをなす方向に直進して蛍光面に当たり、その点を発光させる。このとき発光する点は蛍光面の中心点からx方向に距離X[m]だけシフトした点となる。
なる角度θをなす方向に直進して蛍光面に当たり、その点を発光させる。このとき発光する点は蛍光面の中心点からx方向に距離X[m]だけシフトした点となる。
uとXを表す式の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、電子の静止質量をm[kg]、偏向板のz方向の大きさをl[m]、偏向板の中心から蛍光面までの距離をd[m]とし、l≪dと仮定してよい。また、速度vは光速に比べて十分小さいものとする。
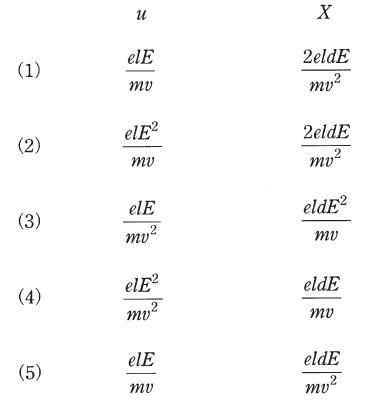
解 説
最初に問われているのは速度uです。速度を求める式で最も有名なのは「速度=距離÷時間」ですが、これは等速運動のときに使う式です。
今回は、x軸方向にだけ注目すると(uがx方向の速度なので)、最初は静止している電子が偏向板を通過する過程で加速し、偏向板を抜けた後は等速運動をするという話で、その加速しきった速度(偏光板を抜けたあとの速度)がuなので、加速度を使った求め方である「速度=加速度×時間」の式を使います。
加速度をa[m/s2]として、問題文の条件から運動方程式を立てると、
![]()
のように、加速度が求められます。
また、偏向板の中を電子が通過する時間t[s]は、z軸方向の長さl[m]と速度v[m/s]から、
![]()
となるので、偏向板を抜けた後のx方向の速度uは、
![]()
と計算できます。
続いてXについて考えます。
問題文よりtanθ=u/vとある一方、図よりtanθ=X/dとなることがわかるので、Xは次の式により求められます。
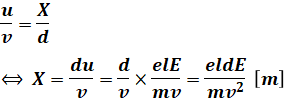

コメント