電験三種 H25年 電力 問9 問題と解説

　問 題　　　　　

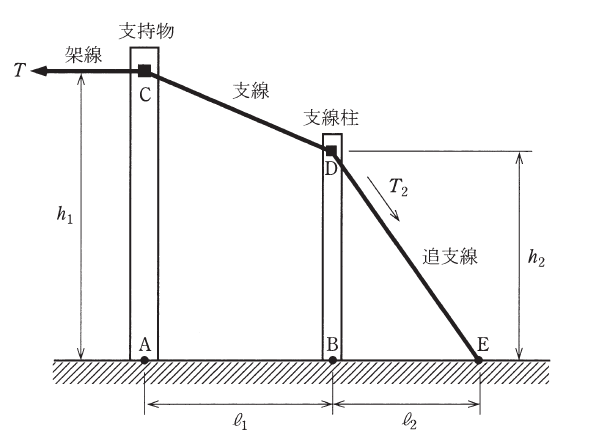
図のように、架線の水平張力T[N]を支線と追支線で、支持物と支線柱を介して受けている。支持物の固定点Cの高さをh₁[ｍ]、支線柱の固定点Dの高さをh₂[ｍ]とする。また、支持物と支線柱の距離ABをl₁[ｍ]、支線柱と追支線地上固定点Eとの根開きBEをl₂[ｍ]とする。

支持物及び支線柱が受ける水平方向の力は、それぞれ平衡しているという条件で、追支線にかかる張力T₂[N]を表した式として、正しいものを次の(1)～(5)のうちから一つ選べ。

ただし、支線、追支線の自重及び掲示していない条件は無視する。

 

 

 

 

 

　解 説　　　　

次の図を使いながら解説します。

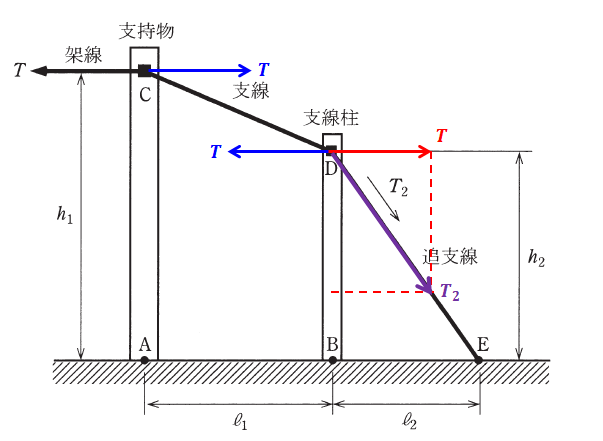
まず、問題文に架線の水平張力T[N]が記入されているので、点Cでは反対方向に同じだけの力が掛かります。すると、また、支線の両端には同じ大きさの力が反対方向に掛かっているはずなので、点DにもT[N]の力が掛かります。ここまでが、上図の青色の2本の矢印です(本当は点Cや点Dに垂直方向の力が掛かりますが省略しています)。

今度は点Dの青矢印に対応する力として、赤矢印が書けます。この大きさは、同じくT[N]です。すると、追支線で点Dを引っ張る力は紫色で示したT₂[N]であることがわかります。

TとT₂の関係は、図のように間の角をθとすると、

となり、一方で、三平方の定理を使うと

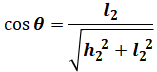
とも表せます。

よって、

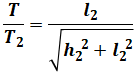
となるので、これをT₂について解けば以下の式が導けます。