電験三種 H24年 理論 問17 問題と解説

　問 題　　　　　

直流電圧計について、次の(a)及び(b)の問に答えよ。

(a)　最大目盛1[V]、内部抵抗r_v=1000[Ω]の電圧計がある。この電圧計を用いて最大目盛15[V]の電圧計とするための、倍率器の抵抗R_m[kΩ]の値として、正しいものを次の(1)～(5)のうちから一つ選べ。

1. 12
2. 13
3. 14
4. 15
5. 16

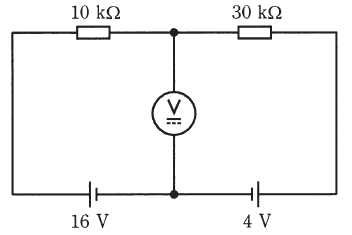
(b)　図のような回路で上記の最大目盛15[V]の電圧計を接続して電圧を測ったときに、電圧計の指示[V]はいくらになるか。最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 7.2
2. 8.7
3. 9.4
4. 11.3
5. 13.1

 

 

 

 

 

　解 説　　　　

(a)

最初の段階で1[V]と1000[Ω]の組み合わせになっているので、これを15[V]に上げるためには、抵抗のほうも15倍して、15000[Ω]にする必要があります。

そのために倍率器を使うのですが、注意点として、ここで15000[Ω]の倍率器を使ってはいけません。15000[Ω]の倍率器を使ってしまうと、もともとの内部抵抗1000[Ω]の分と合わせて16000[Ω]になってしまうからです。

よって、電圧計の内部抵抗と倍率器の抵抗を合わせると15000[Ω]になるように、倍率器の抵抗は14000[Ω](=14[kΩ])にするのが正しいです。

(b)

(b)は(a)の条件(最大目盛15[V])を使うことになっているので、図中の電圧計の部分は15[kΩ]の抵抗として表現できます。

求めたいのは電圧計(図中でいうと15[kΩ]の抵抗)の電圧なので、図中で示した赤矢印と青矢印のそれぞれの回路でキルヒホッフの第二法則を使って式を立て、それらを連立方程式として解くことで、紫色で示した電流値を算出します(ちなみに、抵抗の単位がkΩとなっているので、それと対応させるために電流の単位をmAとしています)。

• 赤矢印の回路

• 青矢印の回路

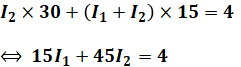
よって、これらの連立方程式を解くと、I₁=0.733[mA]、I₂=-0.155[mA]となるので、I₁+I₂=0.578[mA]です。

以上から、求める電圧は

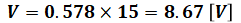
となります。