問 題
三相同期電動機が定格電圧3.3[kV]で運転している。
ただし、三相同期電動機は星形結線で1相当たりの同期リアクタンスは10[Ω]であり、電機子抵抗、損失及び磁気飽和は無視できるものとする。
次の(a)及び(b)の問に答えよ。
(a) 負荷電流(電機子電流)110[A]、力率cosφ=1で運転しているときの1相当たりの内部誘導起電力[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 1100
- 1600
- 1900
- 2200
- 3300
(b) 上記(a)の場合と電圧及び出力は同一で、界磁電流を1.5倍に増加したときの負荷角(電動機端子電圧と内部誘導起電力との位相差)をδ’とするとき、sinδ’の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.250
- 0.333
- 0.500
- 0.707
- 0.866
解 説
三相同期電動機の1相分の等価回路は次のように描くことができます。
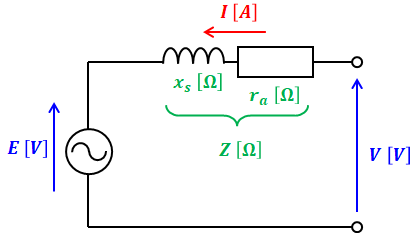
- V:電動機の端子電圧(定格運転時、1相あたり)[V]
- E:内部誘導起電力(1相あたり)[V]
- I:電機子電流[A]
- xs:同期リアクタンス[Ω]
- ra:電機子巻線抵抗[Ω]
- Z:同期インピーダンス[Ω]
(a)
(a)の条件を上図に反映させると、以下の図のようになります(raは問題文により無視できます)。
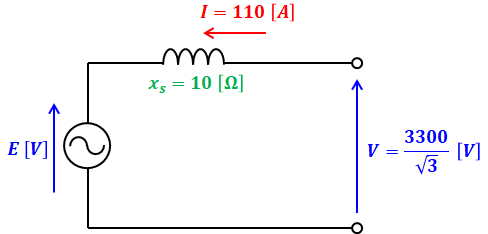
上図において、Vは問題文より力率1で、xsはリアクタンス(力率0)です。そのため、以下のような直角三角形が描けるので、三平方の定理を使えば、1相当たりの内部誘導起電力E[V]を求めることができます。
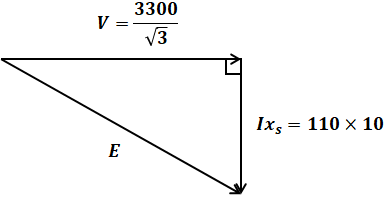
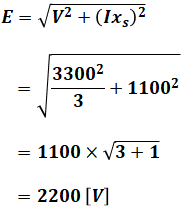
(b)
まず、三相同期電動機の出力は次の式で表されます。これは公式としてぜひ押さえておきたい内容です。
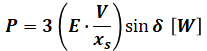
- P:三相同期機の出力[W]
- E:内部誘導起電力[V] (相電圧実効値)
- V:負荷端子電圧[V] (相電圧実効値)
- xs:同期リアクタンス[Ω]
- δ:EとVとの位相角[rad]
ただし、上式の3は三相の3なので、今回は(a)の計算結果を使いたい都合上、1相あたりの出力で計算をしたいので、この3を抜いて以下の式で考えます(この操作をせず、(a)の結果を3倍する解き方でも問題ありません)。
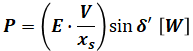
上式のうちP、E、V、xsがわかれば、sinδ’がわかるので、これらの数字を確定させるのがこの問題の解き方の流れです。
まずPについて、問題文よりこの同期電動機の損失は無視できるので、出力P=入力Pinとなります。また、「(a)の場合と電圧及び出力は同一」とあるので、(a)の計算結果を使うことができます。
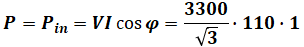
続いて、内部誘導起電力Eは以下の式で表すことができます。
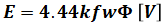
- E:内部誘導起電力[V] (相電圧実効値)
- k:巻線係数
- f:周波数[Hz]
- w:巻数(1相あたり)
- Φ:磁束[Wb](1極あたり)
また、磁束(界磁磁束)は界磁電流にほぼ比例するので、つまり、内部誘導起電力Eは界磁電流に比例するといえます。
よって、界磁電流が1.5倍になれば、(b)でのEの値は、(a)の数値から1.5倍すればよいということになります(下付き文字の(a)、(b)は、それぞれ(a)の条件でのE、(b)の条件でのEということを表しています)。
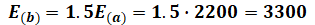
また、Vは問題文の「(a)の場合と電圧及び出力は同一」から、そのままです。
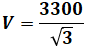
最後のxsについても、(a)や(b)より前の大もとの問題文に「1相当たりの同期リアクタンスは10[Ω]」とあるので、これもこのままです。
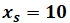
以上の値を公式に代入していくと、求める答えが得られます。
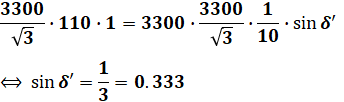

コメント