問 題
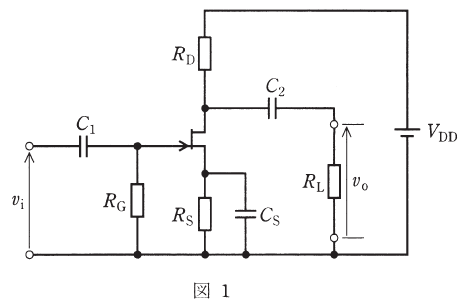
図1は、飽和領域で動作する接合形FETを用いた増幅回路を示し、図中のvi並びにvoはそれぞれ、入力と出力の小信号交流電圧[V]を表す。
また、図2は、その増幅回路で使用するFETのゲートソース間電圧Vgs[V]に対するドレーン電流Id[mA]の特性を示している。
抵抗RG=1[MΩ]、RD=5[kΩ]、RL=2.5[kΩ]、直流電源電圧VDD=20[V]とするとき、次の(a)及び(b)の問に答えよ。
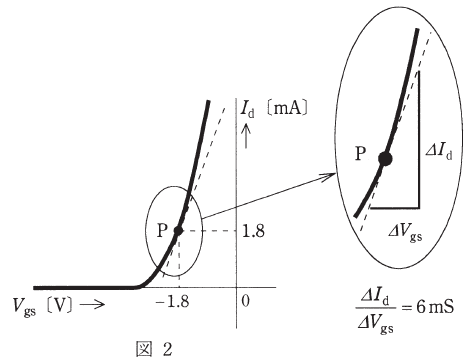
(a) FETの動作点が図2の点Pとなる抵抗RS[kΩ]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.1
- 0.3
- 0.5
- 1
- 3
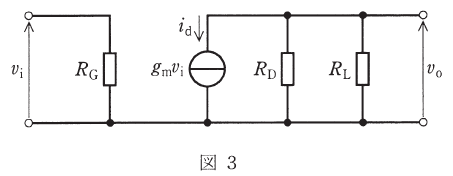
(b) 図2の特性曲線の点Pにおける接線の傾きを読むことで、FETの相互コンダクタンスがgm=6[mS]であるとわかる。この値を用いて、増幅回路の小信号交流等価回路をかくと図3となる。
ここで、コンデンサC1、C2、CSのインピーダンスが使用する周波数で十分に小さいときを考えており、FETの出力インピーダンスがRD[kΩ]やRL[kΩ]より十分大きいとしている。
この増幅回路の電圧増幅度 の値として最も近いものを次の(1)~(5)のうちから一つ選べ。
の値として最も近いものを次の(1)~(5)のうちから一つ選べ。
- 10
- 30
- 50
- 100
- 300
解 説
解説の前に、まずはゲートの役割を確認しておきます。
FETにおけるゲートは、ここに掛ける電圧を大きくしたり小さくしたりすることによって、ドレーンからソースへ流れる電流の大きさを調節することができます。ゲート端子はインピーダンスが非常に大きいため、ここを流れる電流は(ほぼ)0です。
(a)
この問題は図が複雑に描かれていますが、今回はFETを増幅回路として用いているため、ここで気にするべきは直流電流のみなので、図中のコンデンサ部分は気にする必要がありません。コンデンサを無視すると、問題文の図は次のようになります。
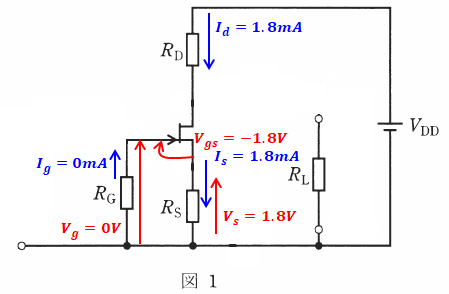
ここで、問題文で与えられている電流値は図2よりId=1.8[mA]ということだけですが、上記の通り、FETではゲートに電流が流れないので、Ig=0[mA]となり、そうすると上図を見てもわかるようにドレーン電流がそのままの大きさでソース電流となるので、Is=1.8[mA]とわかります。
ちなみに、ゲートに電流が流れないことを知らなくても、問題文によるとRG=1[MΩ]、RD=5[kΩ]、RL=2.5[kΩ]なので、ゲート端子のインピーダンスだけ桁違いに大きく、ここを流れる電流は無視できるほど小さいということが判断できます。以上が、上図の青字で記入した内容です。
次に電圧について考えますが、RGには電流が流れないので、赤矢印で示したVgの部分も、当然電圧差はなく、0[V]です。一方、ゲート-ソース間電圧は問題文の図2でVgs=-1.8[V]と与えられているため、両者の差を考えれば、
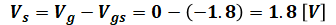
となり、以上から抵抗Rsが次のように計算できます(ちなみに、電流の単位が[mA]なので、抵抗の単位は[kΩ]となります)。
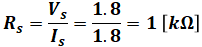
よって、正解は(4)となります。
(b)
図3として等価回路がすでに描かれているのでこれを利用します。求めたいのがvoとviの比ですが、図3の左側にはviしかないのに対して、図3の右側にはvoとviが両方とも使われているため、この問題ではこちら側に注目し、voを、viを含んだ式で表すことを目指します。
まず、RDとRLが並列に並んだままだと考えにくいので、2つの抵抗を合成します。
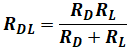
また、図3には電流源がgmviと表されている一方、そこを流れる電流はidと書かれているため、これらは等しいです。
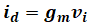
以上をまとめると、図3の右側は次のように描き換えることができます。
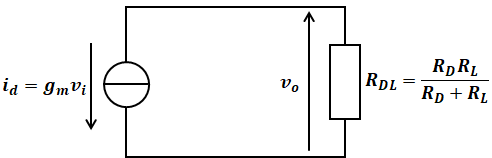
よって、voは次のように計算することができ、求めたい電圧増幅度Avは次の通りとなります。
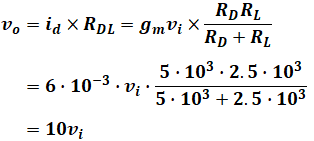
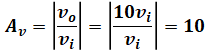
以上から、正解は(1)となります。

コメント