複素数の足し算、引き算、掛け算の計算方法については前項で扱ったので、この項では、割り算のやり方を紹介します。
普通の数字(実数)の割り算の場合、割る数が分母に、割られる数が分子にきます。
![]()
複素数についても同様で、割る数が分母に、割られる数が分子にきます。
![]()
ただし、分母に虚数を含む複素数は計算途中と見なされるので、有理化をして分母を実数のみにしなくてはいけません(もちろん、解答の選択肢で分母が複素数となっている場合には、有理化は必要ありません)。
まず、有理化のやり方の例を以下に挙げます。
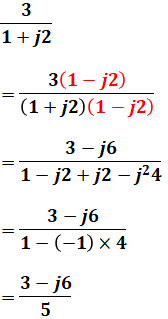
このように、分母に虚数が含まれる場合には、分母と分子の両方に「分母の虚数の符号を反転した複素数」を掛けます。
分母と分子の両方に同じものを掛けているので、全体としてはもともとの値と変わりありませんが、こうすることによって上式のように分母から虚数がなくなるので、虚数が分子にだけ含まれている複素数とすることができます。
また、上記の例では、最初の段階で虚数を含んでいるのが分母のみでしたが、もし分母と分子の両方に虚数があった場合でも、同様で、分母と分子の両方に「分母の虚数の符号を反転した複素数」を掛けます。
つまり、分子が実数であるか複素数であるかは関係なく、とにかく分母に虚数があるかどうかだけ注目すればよいです。この例だと、たとえば次のような計算過程となります。
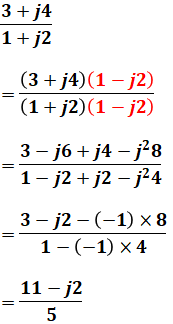
これを一般式で表すと、以下のようになります(ルールさえ押さえておけば、公式として暗記する必要はありません)。
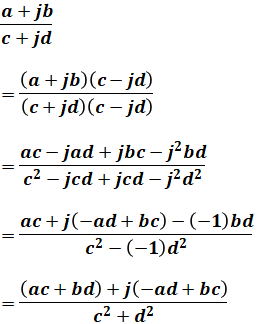

コメント