複素数の和と差
複素数の和と差の計算は簡単です。複素数のうち、実数部(jの付いてない数)と虚数部(jの付いている数)とを分け、実数部同士、虚数部同士は単純に足したり引いたりできる一方で、実数と虚数との間では計算できないというルールです。
たとえば、次のような例を見るとわかりやすいと思います。
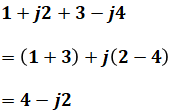
これが文字式になっても、同様の計算をします。
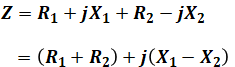
複素数は最終的に2つの項(実数部と虚数部)が残りますが、これら2つを計算することはできないので、これが最終的な式となります。
複素数の積
複素数同士の掛け算をするとき、最重要ルールをひとつ覚えておく必要があります。それは、「j」と「j」を掛けると「-1」になるというものです。「j2=-1」という覚え方でもいいです。
普通の数(実数)は+と+を掛けても+、-と-を掛けても+となりますが、「j」の数(虚数)は、2つ掛けると-になります。
たとえば、
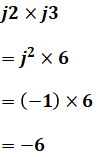
といった感じです。
もう少し複雑な例を挙げると、
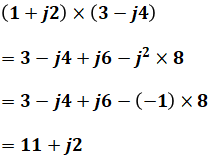
のように計算することができます。ちなみに、上式を見てもわかる通り、実数と虚数とを掛ければ虚数になり、虚数と虚数を掛ければ実数となります。
このように、「j2=-1」となることさえ覚えておけば、そんなに難しいことはないと思います。

コメント