ベクトルの大きさ

ベクトルというのは、向きと大きさを持った値(矢印)のことですが、この項では、その大きさの計算方法を紹介します。

まず、あるベクトルの大きさを知りたいときは、そのベクトルを斜辺とする直角三角形を描きます。

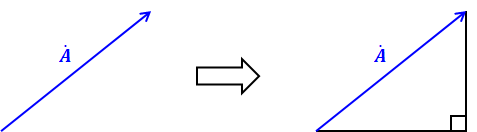
そして、この直角三角形の縦と横の長さがわかるなら、三平方の定理を使えば斜辺の長さが計算でき、また、この斜辺の長さこそがベクトルの大きさであるので、これで解決です。

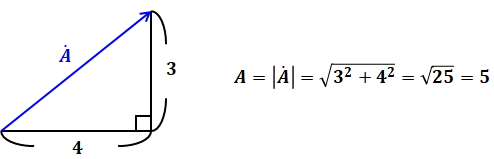
ちなみに、上式の「A」というのはベクトルの大きさを表しています。元のベクトルは向きを持っているためAの上に「・」を付けていますが、ベクトルの大きさを表すときには、単に「A」とするか、もしくは上式第2項のように、ベクトルを絶対値で囲って表すこともあります。

以上で話が終わればよいのですが、実際の計算問題では、そうすんなり直角三角形の縦と横がわからないことのほうが多いです。そのような場合には、三角比を使ってベクトルの大きさを求めることができます。

たとえば、あるベクトルに対して直角三角形を作った結果、次のような数値がわかっているとします。

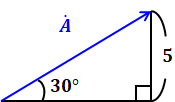
そうしたら、sinθの定義を使って計算することによって、ベクトルの大きさを算出することができます。

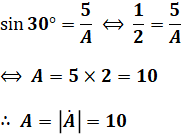
このように、三平方の定理や三角比の計算を用いることで、ベクトルの大きさを求めることができます。